Kursens hemsida    schema
	Aktuell Information

 

Mo 23/1-06

Tentan är nu rättad. Rose-Marie skall föra in resul­taten i LADOK, sedan kan ni se resul­tatet på "mina sidor". Tentorna finns för åter­lämning på student­expedi­tionen.

Vad gäller klagomål ("begäran om om­prövning") av tentor, så notera att bara uppenbara fel­aktig­heter i rätt­ningen skall åt­gärdas av mig; läs här!

Nu är 84 god­kända (31 betyg 3, 43 betyg 4, 10 betyg 5) av 128; 44 är alltså tråkigt nog fort­farande under­kända. Några av er har rätt att komplet­tera; det står på er tenta. Ni som vill det skall kon­takta mig senast 6:e februari.

Torsdag 12/1-06: Lösningar till tentan.

Äsch då. Jag glömde göra lösningar till tentan som gick igår. Här finns de nu.

Och Här är tentan.

Måndag 28/11: tentan rättad.

Tentan är nu rättad. Tentorna finns på student­expeditionen. När Rose-Marie lagt in resultaten i LADOK kan ni se det i "mina sidor". Det gick inte så bra: 52-U, 31-3, 34-4, 10-5. Alltså 59% godkända. Det är bättre än t.ex. Kemi och Elektro, men ändå litet av en besvikelse. Men ni som klarat tentan har gjort det bra!!

Sex stycken har fått femton poäng, och har möjlighet att komplettera till betyget tre. Ni skall kontakta mig senast den 14/12 om ni vill komplettera. PUL förbjuder mig att namnge er här.

Klart, Slut!

Tentamen Måndag 7/11

Lokalen ni tentar i beror på efternamnet:

Abr-Dem  V11

Ded-Han  V21

Has-Lin  V22

Lin-Per  V23

Per-Win  V32

Wus-Åst  V33

Jag vill gärna höra konstruktiva synpunkter på kursen. Speciella frågor:

– Är det lagom med föreläsningar och lektioner, eller skulle det vara bättre med färre sådana och i stället "räknestugor"?

– Läroboken OK?

– Web-sidorna -- OK med information?

– övrigt?

Här är länken till kursenkäten.

Efter skrivtidens slut finns tentan med lösningsförslag här.

Torsdag 27/10

Jag repeterade inte­grations­teknik. Några primitiva funktioner är bra att kunna utantill. Jag tog exempel på trigono­metriska inte­graler (tangens för halva vinkeln) och rot­ut­tryck (då man sub­stituerar med sin, sinh eller cosh.) Det är nog inte helt fel att ta upp detta något mer på lektionen i morgon.

Måndag 24/10

Det var fånigt av mig att tro att jag skulle hinna med något annat än induktions­bevis. Jag gick alltså igenom induktions­bevis, och tog bl.a. exemplet n-te derivatan av en produkt (formel (34) sid 209 i boken.) Induktions­bevis finns litet styv­moderligt behandlat i boken, men det finns en genom­gång som börjar längst ner på sidan 125 med exemplen 61, 62, och 66. Även SATS 17 på sidan 209 bevisas med induktion i boken (samma som jag gjorde på före­läsningen.)

Torsdag 20/10

Jag följde kursplaneringen. Jag fick ont om tid på slutet, så vi får ta det litet noggrannt på lektionen i morgon. Speciellt "resonans" gick väldigt snabbt.

Jag tog upp förskjutningsregeln, som jag formulerade så här: Om vi har en ekvation

y"(x) + ay'(x) + by(x) = e^cx f(x)

så får vi efter substitutionen

y(x) = e^cx u(x)

ekvationen

u"(x) + p'(c) u'(x) + p(c) u(x) = f(x)

där p(r) är karakteristiska polynomet till ursprungliga ekvationen.

Lappskrivningarna

gick bedrövligt dåligt. Av 132 skrivande hade 34 godkänt (två eller tre rätt) på första lappskrivningen, och lika många på den andra. Godkänt på bägge hade 18 stycken.

Vid tentamen kommer det att finnas listor med namnen på dem som har godkänt på någon av lappskrivningarna. Dessa personer har alltså redan uppgift ett och / eller två avklarade på tentan.

Måndag 17/10

Jag började med ett problem där man skulle ta reda på hur lång tid det tar innan saldot på ett bank­konto går ner till noll, om man får konti­nuerlig ränta sam­tidigt som man tar ut pengar i en jämn ström. Vi kom fram till en differen­tial­ekvation, och det föran­ledde mig att ta upp separer­bara differen­tial­ekvationer enligt den här stencilen. Därefter löste vi problemet.

Andra timmen tog jag upp Mercators projek­tion, och "myran på gummibandet" enligt kursplaneringen.

Torsdag 13/10

Jag tog upp ett antal problem som ledde till integraler. Konsument­överskott och tiden det tar för att tömma en tank. Vi räknade explicit på fallet med en sfärisk tank. Jag beräknade också klotets med radie r area och volym. Slutligen härledde jag integral­formeln för båg­längden av en graf y=f(x).

Måndag 10/10

Jag bara repeterade litet om Maclaurin och integraler.

Torsdag 6/10

Jag tog väsentligen upp det som står i kursplaneringen. Jag kom in på generaliserade integraler (kap. 6.5 fram till "Jämförelsesatser".) Jag gör ingen större affär av detta: det är bara att räkna på som vanligt: är intervallet för integra­tionen obe­gränsat tar man gräns­värdet då intervall­gränsen går mot oändlig­heten. Är inte­granden obe­gränsad så räknar man på som vanligt om den primitiva funktionen är kontinuerlig. Det väsentliga är att den primitiva funktionen är kontinuerlig, inte att inte­granden är kontinu­erlig, eller ens begränsad. Det är t.ex bara att räkna som vanligt när man integrerar

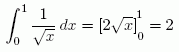
Måndag 3/10

Jag visade formeln för substitu­tion av variabler i integraler. Därefter började jag med en mer systematisk genomgång av medoder för integration.

Först påpekade jag att inte alla elementära funktioner har elementär primitiv. Jag tog exemplet sin(x)/x : den har en primitiv som vi kan skriva som en potens­serie, men den kan inte uttryckas som en elementär funktion.

Därefter började jag med rationella funktioner: först integralen av "elementära bitar", och sedan upp­delning i partial­bråk av rationella funktioner som en summa av "elemettära bitar". Vi tog ett par exempel.

Sista tjugo minuterna tog jag upp trigono­metriska uttryck: jag gick igenom substitu­tionen "tangens för halva vinkeln" och räknade ett exempel. Jag på­pekade att metoden ofta leder till långa räkningar, och att man ofta tar till andra ad-hoc metoder som leder till enklare kalkyler, men jag tog inga sådana exempel (utom integralen av tan(x).)

Vi kan alltså nu öva på integration av rationella funktioner och trigono­metriska uttryck.

Lappskrivning nummer två

tar vi första lektionstimmen onsdagen den 12:e oktober. Den blir på Maclaurin-utvecklingar, (ev. L'Hôpitals regel) och integraler, så långt vi kommit då.

Fredag 29/9

Jag gick igenom Riemann-integralen mer nog­grant än jag planerat, så jag anser det avklarat. Det tog hela första timmen, varför jag fick litet ont om tid att andra timmen gå igenom partiell integration och substitution av variabel.

Jag påpekade att "produktregeln" vid derivation och "kedjeregeln" måste kunna utnyttjas på något sätt vid integration. Det ger "partiell integration" respektive "substitution av variabel". Jag här­ledde regeln för partiell integration och tog ett par exempel, både på obestämda och bestämda integraler.

Jag kom i tidsnöd, och valde att inte göra någon härledning av "substitution av variabel", utan jag skrev upp formeln (bestämd och obestämd integral) och räknade ett par exempel. Exemplen visade regeln ut­nyttjad åt bägge hållen dvs. ibland har man ett uttryck t.ex.

sin(x)·cos²(x)
och man sätter

sin(x)=t
Men man kan också ha t.ex. uttrycket

(1-x²)^1/2
och man går då åt andra hållet och sätter

x=sin(t)
Det gick ganska fort, så vi får ta det lugnt och noggrannt på lektionen i morgon!

Tisdag 27/9

Jag tog först ett par exempel på Taylor-utvecklingar kring andra värden än x=0. Vi tittade på sin(x) kring x = π/3 och x^1/2 kring x = 4.

Jag tog upp resttermen i Maclaurin:
– Bevis för "ordo-varianten" (men inte begreppet ordo,)
– Lagranges restterm, och
– den exakta integral-varianten.

Vi använde Lagranges restterm för att visa att Maclaurin-serien för sin(x) konver­gerar (mot sin(x)) för alla x. Därefter påpekade jag att Maclaurin­serierna för cos(x), exp(x), sinh(x) och cosh(x) också konver­gerar mot respek­tive funktions­värde, och att de övriga i utantill-listan (ln(1+x) osv.) konvergerar för –1 < x < 1 (jag bryr mig inte om rand-fallen.)

Vi använde dessa serier för att ta fram serier som konver­gerar mot π/4   (arctan(1/2) + arctan(1/3)) och ln(3)   (ln(1+x) – ln(1–x) med x=1/2.)

Fredag 23/9

Jag gick igenom Mac­laurin­utveck­lingar, men bara med rest­term av typen c(x)·xⁿ, (alltså av typen stort ordo) där c(x) är kontinu­erlig i x=0. Jag här­ledde väsent­ligen alla de vanliga Mac­laurin­utveck­lingarna; se "utantill-"stencilen.

Jag räknade dels ett enkelt gräns­värde av typen 0/0 (som man lika gärna kan lösa med L'Hôpitals regel) men också ett par andra exempel: vi såg att

(n³+n²)^1/3 - n = 1/3 - 1/(9n) + c(1/n)·(1/n²),

och jag visade att om vi står på ett torn med höjden h så är av­ståndet från tornets fot till hori­sonten approxi­mativt (2·r·h)^1/2   (r=jordens radie.) Detta genom att approxi­mera

cos(v) och 1/[1+(h/r)]

med deras respek­tive Mac­laurin­utveck­lingar.

Jag tog inte upp utveck­lingar kring andra punkter än x=0.

Onsdag 21/9

Bara repetition. Litet om faktor­satsen, heltals- (och rationella) rötter till polynom med heltals-koeffici­enter, Algebrans funda­mental­sats. Något om binomial­koeffici­enter och binomial­satsen, och någre exempel på arcus­funktio­nerna.

Måndag 19/9

Jag gick igenom kapitel 4, utom 4.5. Jag började med kapitel 4.6 och visade satsen i min stencil om konvexa och konkava funktioner. Jag illustrerade med ett par enkla exempel.

Därefter tog jag upp resten av kapitlet genom att demonstrera ett antal exempel; dela några enkla från Broneks "dagens", dels ett par mer krävande exempel: "stegen i korridoren" och exemplet 9 på sidan 227 i boken.

Torsdag 15/9

Jag visade först satsen att deri­vatan i en extrem­punkt är noll. Därefter visade jag differen­tial­kalkylens medel­värdes­sats. Jag följde i stort sett fram­ställningen i kapitel 3.5.

Sedan visade jag korol­lariet att positiv deri­vata innebär växande funktion, och negativ deri­vata av­tagande funk­tion. Som exempel gjorde jag "tecken­tabell" för funktionen

y = x exp(-x)

och skis­serade dess graf. Sedan tog vi paus.

Andra timmen ägnade jag i stort sett åt L'Hôpitals regel. Först räknade jag ett par exempel på gräns­värden, även exemplet

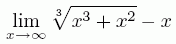
varpå jag drog beviset för L'Hôpitals regel enligt min stencil.

Vi hade några minuter kvar, så jag passade på att bevisa att om andra-derivatan är negativ så är funk­tionen konkav, i meningen att varje korda ligger under funk­tionens graf.

Tisdag 13/9

Jag följde kurs­planeringen. Första timmen defini­erade jag deri­vatan och härledde deri­vatan av sin(x) och ln(x). Jag skrev upp deri­verings­reglerna för summa, diffe­rens produkt och kvot, och för samman­satta funk­tioner ("kedje­regeln".) Jag bevisade formeln för deri­vatan av produkt.

Gymnasiet är nuför­tiden bra på att lära ut tolk­ningar av deri­vatan, så jag upp­manade bara studen­terna att på­minna sig detta.

Andra timmen tog jag upp kedje­regeln i detalj och räknade ett par ganska enkla exempel (i en del skolor tar de inte upp kedje­regeln helt generellt, trots att det ingår i studie­planen för mate­matik C och D.) Sedan tog jag upp impli­cit deriva­tion, och an­vände det för att deri­vera y(x) = exp(x): jag deri­verade identi­teten ln(y(x)) = x m.a.p. x. Sedan deri­verade jag x^x genom att logarit­mera och deri­vera implicit. Slut­ligen här­ledde jag deri­vatorna av arcsin(x) och arctan(x) på samma sätt: y(x)=arcsin(x) innebär att sin(y(x)) = x som vi deri­verade implicit, o.s.v. Jag skrev alltså inte upp någon formel för in­versens deri­vata, utan jag deri­verade implicit i stället. Jag ifråga­satte aldrig om inversen ö.h.t. var deriver­bar.

Lappskrivning 1

kommer att vara första timmen av lektionen torsdagen 22/9. Det blir tre uppgifter inom något område vi läst tom. vecka 37. Två rätt lösta uppgifter ger första uppgiften på sluttentan.

Fredag 9/9

Jag tog upp defini­tionen av gräns­värde (def. 1 sid 132 och (5) sid 134) och illus­trerade med några enkla exempel (för varje ε>0 finns δ>0 osv.) Jag passade på att ta upp litet om implikationer (skillnaden mellan "om" och "endast om") och kontrapositiva formuleringen. Jag tog dock inte exemplet

If the ocean was whiskey
and I were a duck
I'd dive to the bottom
and never come up

som har kontrapositiven

If I never reach bottom
or sometimes come up,
then the ocean isn't whiskey
or I'm not a duck.

(Jag minns inte var jag läst detta,) utan ett något enklare exempel.

Jag nämnde defini­tionen av kontinu­erlig funktion, och sa att alla elemen­tära funk­tioner är kontinu­erliga där de är defini­erade, så vi skall inte behöva larva oss med gräns­värdet av x² när x —>2, osv. Jag tog upp satserna 2, 3, 4 på sid 136, och "Haralds Lemma" (se kursplaneringen,) men bevisade inget av dem. Däremot bevisade jag det viktiga gräns­värdet SATS 14 sid 114 (i kap. 1.9,) men inte som i boken (det "beviset" är inget bevis!) utan genom att jämföra areor. Jag bevisade också gräns­värdet (21) sid 154, men igen genom att jäm­föra areor (ln(x) är arean under 1/t från 1 till 1+x.) Slutligen tillämpade jag "Haralds Lemma" genom att härleda gränsvärdet (18) sid 153 genom att först ta logaritmen för uttrycket.

Onsdag 7/9

Jag förutsätter att alla kan räkna med logaritmer och exponential­funktioner. Jag vet å andra sidan att detta inte är helt realistiskt, så kontrollera att du kan lösa uppgifterna 1.24, 1.25, 1.26, 1.29, 1.31. Har du problem med dem (det är det säkert många som har,) så fråga lektions­läraren. Det kan vara lämpligt att ta upp några av dessa upp­gifter på lektionen!

Jag följde kurs­plane­ringen, dvs. jag repe­terade kort räkne­reglerna för exp och log. Därefter defini­erade jag de hyper­boliksa funk­tionerna, och påpekade att

(cosh(x), sinh(x))

ligger på hyperbeln

x² – y² = 1

Sedan visade jag att exponential­funktioner växer snabbare än polynom, och att logaritmer växer lång­sammare än polynom; en slags "standard­gräns­värden" alltså.

Därefter nämnde jag snabbt att y=e^x är ekvivalent med att x = ln(y), och att detta kallas att exponentialfunktionen och logaritmen är varandras inverser. Sedan definierade jag arcsin, arccos och arctan, och ritade deras grafer. Jag löste också ett enkelt problem av typen bestäm värdet av arcsin(a) + arcsin(b). Eftersom a och b var positiva, och a² + b² = 1 såg vi att

arcsin(a) + arcsin(b) = π/2.

Till sist gav jag som övning att visa att

arctan(1/2) + arctan(1/3) = π/4.

Måndag 5/9

Jag beklagar att det här kommer sent. Jag tog upp Pascals Triangel, och visade att binomial­koeffici­enterna som upp­träder där kan tolkas som antalet sätt att välja ut k objekt bland n stycken, utan åter­läggning och utan hän­syn till ord­ning. Jag visade sedan Binomial­teoremet.

Andra timmen pratade jag om polynom. Jag visade faktor­satsen och det uppen­bara resul­tatet att för ett polynom med hel­tal­skoeffici­enter gäller att en heltals-rot måste vara en faktor i konstant-termen. Vi använde detta för att faktori­sera polynom.

Jag skrev också upp den reella vari­anten av Algebrans Funda­mental­sats: Varje reellt polynom kan faktori­seras (på väsent­ligen ett unikt sätt) i första­grad­sfaktorer och irredu­cibla andra­grads­faktorer (andra­grads­polynom som saknar reella noll­ställen.) Vi faktori­serade polynomet

x⁴ + 4 = (x² + 2 x + 2)·(x² – 2 x + 2)

genom att ansätta en faktor

x² + a x + b

och utföra divi­sionen. Kravet att denna skall ge resten noll gav värden på a och b. Jag nämnde att på lek­tionerna skulle studen­terna säkert få demon­strerat hur man kan använda komplexa noll­ställen för att utföra faktori­seringen.

Torsdag 1/9

Första timmen pratade jag om summa­symbolen, teleskoperande summor, och geometrisk summa. På slutet löste jag följande problem: säg att man varje månad sätter in a kronor på ett bankkonto, med första inbetalningen månad 1. Antag att räntan är r per månad. Vad är då saldot S(n) efter n månader? Det gick väldigt fort. Resultatet var iaf.

S(n) = (a/r)·([1+r]ⁿ – 1).

Andra timmen ägnade jag åt komplexa tal. Jag införde "komplexa talplanet" som en ut­vidgning av "reella tallinjen" och definierade multi­plikation geo­metriskt. Sedan visade jag att algebraiskt innebär detta att man multi­plicerar enligt distri­butiva lagen och använder i² = –1. Jag tog alltså upp polär framställning, men inte Eulers formler — det får vi göra på lek­tionen i morgon.