Kursens hemsida    schema
	Kursplanering

 

Inneåll

Jag planerar att i stort sett följa bokens framställning. Men jag kastar ändå om ordningsföljden i några fall.

Min erfaren­het är att hur många övnings­uppgifter jag än före­slår i kurs-PM:et så kommer studen­terna ändå att fråga efter fler. Därför anger jag groteskt många upp­gifter i hopp om att det skall räcka åtmin­stone till en början. Sedan får lektions­lärarna själva välja bland dem att ta upp på under­visningen. Om studen­terna vill ha ett urval bland dem som är kvar att räkna hemma, så hoppas jag lektions­lärarna hjälper till med detta. Jag menar allstå inte att man skall räkna samt­liga före­slagna upp­gifter, utan studen­terna själva, ev. i samråd med lektions­lärarna, gör ett urval.

Det är alltså givetvis inte meningen att man skall gå igenom alla de upp­gifter som finns listade på lektionen, utan läraren gör ett urval, och är fria att använda andra också. Bland de åter­stående kan studenterna välja problem för själv­studier.

Kurs­planeringen är dynamisk — dvs. den kommer säkert att ändras efter hand. Det är förmodligen olämpligt att låsa fast plane­ringen helt från början.

Vecka 35

Fö.  1/9 Komplexa tal, summa­symbolen; teleskoperande summor, geometrisk summa. Appendix A.1 – A.7, B.3; kap. 1.4.4.

Le.  2/9 Observera att jag inte hann med Eulers formler; det får vi ta upp på lektionen. Se "Aktuellt".

Problem: Vilka problem som är lämpliga beror på om studenterna läst Matematik E på gymnasiet eller inte. Var flexibla! Förslag: A.10, A.12, A.17, A.18, A.20, A.21, A.22, A.28, A.30.
1.85–1.93.
Visa med teleskoperande summor att
a) 1·4 + 2·7 + 3·10 + · · · + n(3n + 1) = n(n + 1)²   för n = 1, 2, 3,....
b) 1³ + 3³ + 5³ + · · · + (2n – 1)³ = 2n⁴ – n²   för n = 1, 2, 3,....

Vecka 36

Fö.  5/9 Polynom, binomialkoefficienter, Pascals triangel, binomialsatsen. Kap 1.4.3, A 10, 1.4.5.

Le.  5/9 problem: 1.16 – 1.19, A.52, A.53, A.54, A.55, 1.94 – 1.103, 1.108, 1.109. Till lärarna: Ta gärna upp några kombina­toriska problem i samband med binomial­koefficienter. Litet konstigt att det inte finns något sådant i övnings­boken.

Fö.  7/9 Kapitel 1.6 och 1.7 handlar om potens- och exponentialfunktioner och logaritmfunktioner. Detta skall vara känt från gymnasiet, så jag lämnar detta för självstudier och föreläser bara på kap. 1.6.4 och 1.7.3: Jämförelse mellan log-, potens- och exponential-funktioner. Dessutom tar jag upp hyperboliska funktioner (1.11); inversa funktioner (1.8.1) och arcus­funktionerna (cyklo­metriska funk­tionerna) (1.10)

Le.  8/9 Problem: 1.41, 1.42, 1.44, 1.46, 1.69–1.84.

Till lärarna: kasta inte om variablerna när ni tar fram inverser. Tyvärr gör boken det, och det är mycket förvirrande. Dvs. inversen till y=x² är x=y^1/2, inte y=x^1/2. Sambandet mellan en kvadrats area A och sidlängd L är A=L², och ingen tillämpare av matematik skulle påstå att det inversa sambandet är att A=L^1/2.

Fö.  9/9 Gränsvärden (2.1), definition av konti­nuitet (två första sidorna av 2.2), standard­gräns­värden (2.4), speciellt (71) sid 114 och (21) sid 154. Den använd­bara satsen ("Haralds lemma") som inte finns i boken:

Om f(y) är en strängt växande funktion, och

f(y(x))—>f(A) då x—>a

så gäller att

y(x)—>A då x—>a.

(Observera att funktionen f(y) inte behöver vara kontinuerlig i Haralds lemma; det räcker att den är strikt monoton.)

Vecka 37

Le.  12/9 Problem: 1.37, 1.39, 2.20b. Gå igenom begreppet asymptot och gör några av uppgifterna 2.24 – 2.27. (Vi tar upp gränsvärden mer efter derivator.)

Fö.  13/9 Kap. 3.1–3.4: derivator; definition, tolkning och räkne­regler. De elementära funktio­nernas derivator.

Le.  14/9 Problem: 3.9, 3.10, 3.12, 3.18, 3.22, 3.31, 3.5–3.8, 3.15, 3.16, 3.20, 3.30.

Fö.  15/9 Kap.3.5, 3.6: medel­värdes­satsen och dess följd­satser; L'Hôpitals regel; högre derivator. (Länk till biografi om Guillaume François Antoine Marquis de L'Hôpital)

Le.  16/9 Problem: Beräkna följande gränsvärden med hjälp av L'Hôpitals regel: 2.4, 2.5d,f, 2.14, 2.15a,b, 2.17. (Då x går mot oändl. sätter man t=1/x, gör så i 2.17 t.ex.)

Det är mycket viktigt att man lär sig derivera. Fortsätt med övningarna från 14/9, och om de inte räcker kan vi ta även Broneks Dagens 10/9.

Lappskrivning 1 kommer att vara första timmen av lektionen torsdagen 22/9. Det blir tre uppgifter inom något område fram tom. ovanstående. Två rätt lösta uppgifter ger första uppgiften på sluttentan.

Vecka 38

Veckan störs av lapp­skrivningen på torsdag. Det är förmodligen psyko-dedaktiskt irrekommen­dabelt att gå igenom något viktigt nytt material innan lapp­skrivningen. På före­läsningen måndag 19:e går jag därför igenom kapitel 4, utom 4.5 som vi inte läser. Materialet där är inte väsent­ligen nytt, utan tillämpar det vi gjort tidigare. Avsnittet om konvexa och konkava funk­tioner (kap. 4.6) är dock väsent­ligen nytt och en aning tekniskt, varför jag skrivit en stencil om detta. Jag tror jag hoppar över "Jensens olikhet" ((14) s. 242), även om den är trevlig, men den är inte speciellt central i den här kursen. På före­läsningen onsdag 21:a (dagen före lapp­skrivningen) blir det nog litet allmän repetition, och så avsluter jag med de viktiga Maclaurin-utveck­lingarna på fredag 23:e.

Vad gör vi då på lektio­nerna? Vi har två lektioner: måndag 19:e och torsdag 22:a. Torsdag 22:a har vi lapp­skrivning första timmen och andra timmen går vi natur­ligtvis igenom den. Men det blir tid kvar. Problem: 4.1–4.41 utom 4.39 (jag tänker ta upp "problemet med stegen i korridoren" på före­läsningen.) Dessa upp­gifter gäller för måndags- och torsdags­lektionen, men om det finns behov är det natur­ligtvis fritt att ta upp gammalt material (inför lappskrivningen.)

Vecka 39

Le.  26/9 Problem på Maclaurin (notera att jag använt beteckningen c(x)·xⁿ,  c(x) kontinuerlig för x=0,   för resttermen:) 9.21 – 9.36.

Fö.  27/9 Mer om Maclaurinutvecklingar. Lagranges restterm, Maclaurin-serier. Utveclkingar kring andra värden än x=0. Obs! För att utveckla kring x=a inför jag en ny variabel t=x-a och utvecklar kring t=0.

Le.  28/9 Gör ett par uppgifter där man uppskattar resttermen i Maclaurin, t.ex. 9.14 och 9.16. Gör också någre exempel på utvecklingar kring ett annat värde än x=0, t.ex. 9.7 plus egna påhitt (det finns för få exempel i häftet.) Jag gör så att jag inför en ny variabel t
    x=a+t
för att utveckla kring x=a.
Ta också upp några av Maclaurin-serierna 9.37–9.39.
Finns det till äventyrs tid kvar fortsätter vi med uppgifterna 9.21 – 9.36, och vi kan också ta t.ex. några lämpliga av 9.40–9.48.

Fö.  29/9 Kapitel 5.1: Primitiva funktioner ("anti-derivator",) partiell integration och substitution av variabler. D:o även för bestämda integraler: vi tar SATS 10 i kap. 6 som definition av bestämd integral, jag tar något upp tolkningen som Riemann-summa. Därmed tar jag också upp sid 300 och 301 fram till kap. 6.5. Notera primitiverna i utantill-listan

Le.  30/9 Problem: välj bland 5.1–5.14, 5.16. Få med både partiell integration och variabelbyte.
Men vi behöver också några bestämda integraler! Det är egendomligt att det inte finns några lätta sådana i övnings­häftet. Gör 6.44 (med variabel­substitution så det framgår hur man ändrar gränserna för integrationen.) Gör dessutom några av upp­gifterna 5.12–5.14, 5.16 som bestämda integraler med några lämpliga gränser. Vi måste visa hur man hanterar gränserna vid partiell integration och substitution av variabler.

Vecka 40

Fö.  3/10 Integrations­teknik. Jag gör så långt jag hinner av kapitel 5.2 (ratio­nella funk­tioner,) 5.4 (Trigono­metriska funk­tioner) och 5.3 (vissa ro­tuttryck.) Jag tar dock inte upp alla speciella fall, utan håller mig till fallen jag beskriver i den här stencilen.

Lappskrivning nummer två

tar vi första lektions­timmen onsdagen den 12:e oktober. Den blir på Maclaurin-utvecklingar, (ev. L'Hôpitals regel) och integraler, så långt vi kommit då.

Le.  5/10 Problem: 5.17–5.26,  5.31,  5.32 b,c,d,f,   5.34,  5.36,  5.37,  5.39,  5.40.

Fö.  6/10 Mer om integraler: jag tar upp "vissa rotuttryck" enligt stencilen och några av integralerna i utantill-listan. Sedan tar jag upp problemet med diskontinuerlig primitiv: t.ex. funktionen

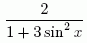
som har "primitiven"

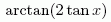
vilket skulle ge den felaktiga uträkningen

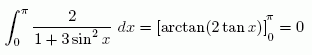
Däremot går det bra att beräkna (den generaliserade) integralen

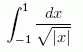
med hjälp av den kontunuerliga primitiven

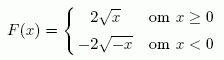
trots att integranden inte existerar för x=0.

Därmed kommer jag in på generaliserade integraler.

Le.  7/10 Fortsätt med problemen på rationella integrander och trigonometriska uttryck. Fler problem: 5.27 a,b,   5.28–5.30, 6.24–6.29.

Vecka 41

Fö.  10/10 Jag går inte igenom nå't nytt, utan repeterar litet. På onsdag har vi lappskrivning.

Le.  12/10 Lappskrivning första timmen. Andra timmen går vi igenom den, sedan fortsätter vi med integrler; glöm inte generaliserade integraler.

Fö.  13/10 Jag börjar nu på kapitel 7: användningar av integraler. Jag tar upp även andra tillämpningar än de geometriska som finns i boken, bl.a. det som i nationalekonomi kallas "konsumentöverskottet" och problemet "hur lång tid tar det att tömma en vattentank via ett hål i botten".

Le.  14/10 Vi löser problem på "tillämp­ningar av integraler". Jag har inte gått igenom kurvor på parameter­form, inte heller polära koordinater, så vi tar inga sådana upp­gifter. Vi förut­sätter inte heller några utantill-kunskaper typ "rotations-volym", utan gör en heuristisk här­ledning i varje enskilt fall — det är sättet att resonera sig fram till en korrekt integral som är det väsentliga, inte formel- kunskaper!

Problem: 7.1 – 7.22, 7.25, 7.26, 7.31 – 7.34, 7.50, 7.52, 7.54 – 7.59, 7.61, 7.64 – 7.67, 7.69, 7.70

Vecka 42

Fö.  17/10 Jag går igenom separer­bara differential­ekvationer och räknar en del tillämpnings­exempel på sådana och mer "tillämp­ningar av integraler" (alltså fort­sättning på förra före­läsningen.) Här är en stencil om separarbara differential­ekvationer såsom jag framställer dem; i boken behandlas de i kapitel 8.3. Jag tar bl.a. upp mot­svarig­heten till problemen 7.12 (snigeln på gummi­snodden) och 7.6 (Mercators projek­tion) i Eike Petermanns bok "Analytiska metoder I". Jag beräknar också hur lång tid det tar för saldot på ett bank­konto att gå ner till noll, om man tar ut en jämn ström samtidigt som man får kontinu­erlig förränt­ning.

Det är möte med fakultetskollegiet direkt efter föreläsningen, så jag kommer inte att hinna skriva något under "Aktuellt" förrän sent på kvällen.

Le.  18/10 Fortsätt med övningarna från i fredags. Observera att ett alternativt sätt att härleda den relevanta integralen är att först formulera problemet som en separerbar differential­ekvation, och sedan lösa den; se den här stencilen som jag tog upp igår. Vi bör visa både metoden med Riemann-summor och metoden via differential­ekvationer — kanske tom. samma problem med bägge metoderna.

Vi tar sedan problem på separer­bara differential­ekvationer: 8.21 – 8.33

Fö.  20/10 Jag börjar på andra ordningens differen­tial­ekvationer (vi tar inte upp 1:a ord­ningens linjära,) dvs. kapitel 8.5–8.7. Vi tar bara upp högerled av typen

A·e^ax cos(bx) och A·e^ax sin (bx)

(även fallet b=0.) Jag substi­tuerar då den okända y(x):

y(x) = e^ax u(x)

och får en diff-ekvation i u(x) med ett höger­led utan exponential-faktor. Se under "aktuellt"! Vi tar givet­vis även upp fallet med resonans. Jag kommer inte att använda komplexa exponential­funktioner, eftersom många inte läst matte E, och är ovana vid att räkna med komplexa tal.

Le.  21/10 Problem: 8.38 – 8.45,   8.49a,   8.51 a,b,c,   8.55,   8.56 – 8.60.

Vecka 43

Fö.  24/10 Jag går igenom induktions­bevis, och gör givet­vis ett par exempel. Jag tror inte det tar hela tiden, så jag hinner förmod­ligen också räkna på en svängande pendel (svängnings-perioden dels approxi­matiivt — diff-ekvation med konstanta koeffici­enter,) dels exakt (elliptisk integral av första slaget.)

Le.  24/10 Räkna de exempel som finns på induktions­bevis i övnings­häftet. Det bör går fort, för det finns inga! Nu står det dock med all oönskad tydlighet i studiehandboken att induktions­bevis ingår i kursen. Vi kan ta de exempel som Bronek har i dagens, vi kan också hitta på några egnea eller ta bland ex­tentorna, tex. uppgift 9 och uppgift 2

Vi kan också fortsätta med andra ord­ningens diff-ekvationer.

Le.  26 och 28/10 Jag beklagar att jag kommit efter med detta. Nu återstår bara repetition. Här är tillsvidare litet grand om vad jag tror vi behöver repetera. Jag skall lägga ut mer material så snart jag hinner.

Fö.  27/10 Jag repeterar integrationsteknik, dock inte själva proceduren att dela upp i partialbråk — det lämnar jag till lektionerna — men integrering av uttrycket man kan få med ett irreducibelt andra­grads­polynom i nämnaren. Jag tar också upp trigonometriska uttryck och "vissa rotuttryck" och kanske någon volymsberäkning.

Vecka 44

Fö. och Le.  31/10.  På före­läsningen tänker jag ta upp exempel på implicit deri­vering, L'Hôpitals regel och Maclaurin­utvecklingar. Det kan nog vara motiverat att något ta upp detta även på lektionen, om studenterna tycker det. Men jag kommer där (också) att ta upp max-min-problem och kanske något exempel på skissning av kurvor. Jag gör också ett exempel på att jämföra en summa med en integral; det blev aldrig av tidigare.

Det är möjligt att vi också behöver repetera något om binomial-teoremet och binomial­koeffici­enter. Vi får känna av vad studenterna vill.

Fö.  1/11 Jag planerar att gå igenom den här modell-tentan. Det är inte en riktig modell­tenta — visser­ligen kan var och en av upp­gifterna finnas på en tenta, men knappast samman­ställ­ningen.