Kursens hemsida    schema
	Aktuell Information

 

Svaren på senaste tentan.

Sista uppgiften skiljer, dock. Här är svaret på den uppgiften:

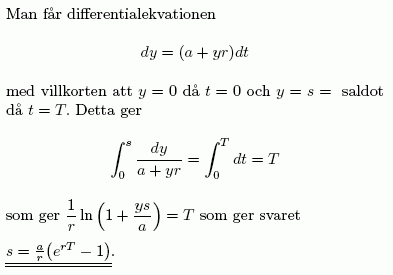
Nu är även era tentor (tentan för Öppen) rättade.

Fredag 19/11

Nu är tentan färdig­rättad. Matte­institutionen har HELA LISTAN på anslags­tavlan. 70% godkända, det är ett mycket bra resultat jämfört med andra programs. Mvh —Harald

Regler för omprövning av betygsbeslut.

Lösningar till tentan 8/10-04

Jag kan inte säga när tentan kommer att vara färdig­rättad. Det pågår ju under­visning som vi lärare är in­blandade i, och vi måste i första hand sköta den. När rätt­ningen är klar med­delar jag det här.

Tisdag 2/11

Jag gick igenom modell­tentan. Någon frågade om jag har en stencil om tele­skoperande serier. Här är en stencil jag skrev för ett par år sedan.

Fredag 29/10

Jag bara löste upp­gifter på differen­tial­ekvationer av första ordningen. Därvid fick vi också en del övning i inte­grations­teknik. Jag gjorde upp­gifterna 8.28, 8.68 , 8.76, 8.80 och 8,82. I samband ned 8.80 påpekade jag att det är lätt hänt att man missar en konstant­lösning när man har en ekvation av typen

y'(x)=f(y)*g(x).
Om f(c)=0 för någon konstant c är ju

y(x)=c
en lösning som man missar om man sepa­rerar variablerna, eftersom man "dividerar med noll".

Torsdag 28/10

Jag såg att uppgift 6 i modelltentan blev dålig — integranden är ju inte definierad i x=0. Jag har ändrat uppgiften nu så att integlalen går från x=1: Modelltenta.

Måndag 25/10

Jag följde kurs­planeringen. Jag tog dock inte upp här­ledningen av rest­termen i Mac­laurins formel; det kan den intres­serade finna i den här stencilen.

Jag tog först upp inte­gral­kalkylens medel­värdes­sats (SATS 7 sid 294), och löste uppgift 6.6. Sedan deri­verade vi inte­graler: 6.12aa,d. Det gjorde jag så att jag kallade en primitiv till inte­granden för F(t), sedan deri­verade vi (i fallet 6.12b) F(sin x) - F(cos x) där vi insåg att vi inte behöver känna till F(X), bara derivatan F'(x).

Därefter tog jag upp generali­serade inte­graler med positiv inte­grand och summor med posi­tiva termer. De antingen konver­gerar eller diver­gerar mot oändlig­heten. Jag löste upp­gifterna 6.30a,b. Där­efter jäm­förelse mellan inte­graler och summor: SATS 1 sid 341, och mot­svarig­heten för växande funktioner. Jag illu­strerade med EXEMPEL 22 sidan 344. Därefter här­ledde jag den enkla varianten av Stirlings formel som finns i utantill-listan genom att an­vända SATS 1 tillämpad på f(x) = ln(x).

Modelltenta

Jag har blivit ombedd att göra en "modelltenta". Den här kanske blev svår i överkant, men det framgår iaf. hur tentan ungefär kommer att se ut. Den skiljer sig alltså inte från andra tentor på den här kursen på annat sätt än att tonvikten kan ligga litet annorlunda, eftersom vi använder en annan lärobok.

Onsdag 20/10

Jag gick igenom även linjära differential­ekvationer av första ordningen (jag hade missat att det finns med i boken.) För övnings­lärarnas skull:

Jag använde följande beteck­ningar: Vi har en differential­ekvation av typen

y'(x) = f(x)y(x) + g(x)

Vi definierar v(x) genom

y(x) = exp(F(x))v(x)     (1)

där F(x) är någon primitiv till f(x). När vi deriverar detta får vi ett uttryck för y'(x) och när vi sätter detta lika med högerledet i differential­ekvationen tar två termer ut varandra, och vi får att

exp(F(x))v'(x) = g(x)

Härur får vi ett uttryck för v'(x) som vi inte­grerar (med inte­grations­konstant!) och sätter in i (1) för att få y(x).

Det finns andra beteck­nings­sätt, och vi får använda vilklet ni vill, men så här gjorde jag på före­läsningen.

Jag tog också upp separer­bara differential­ekvationer (av första ordningen) och ett par enkla exempel. Jag tog också upp lösning­arna till homo­gena andra ordn­ingens differen­tial­ekvationer med konstanta koeffici­enter; de tre fallen fallen: rella olika, reella lika, och komplexa rötter till karak­teristiska ekvationen. Jag bevisade fallet med reella rötter, fast i ett numeriskt exempel, för att det skulle vara litet lättare att följa ("reduktion av ordning".)

Fredag 15/10

Jag tog först ett exempel på integral, där vi bestämde tiden för en vätska att rinna ur ett kärl. Sedan tog jag upp gene­rali­serade inte­graler. Först fallet med obe­gränsad inte­grand. Först tog jag det knäppa exemplet

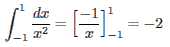
Jag påpekade att då inte­granden är obe­gränsad fun­gerar inte defini­tionen av integral som gräns­värdet av en Riemann-summa, så man defini­erar den generali­serade inte­gralen som ett gräns­värde av Riemann-integraler. Resul­tatet är att man kan räkna på som vanligt så länge den primi­tiva funk­tionen är konti­nuerlig. Exempel:

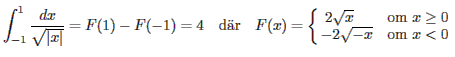
fast jag tog bara inte­gralen från 0 till 1. Sedan tog vi inte­graler med obe­gränsat inter­vall. Jag gjorde också ett exempel då man får en generali­serad inte­gral efter en substi­tution; uppgift 6.39, fast vi inte­grerade bara från 0 till p.

Jag tog som hastigast upp integralkalkylens medelvärdessats (inte den generella) och löste uppgift 6.5.

Jag tog inte upp jäm­förelse inte­graler—summor; inte heller någon­ting om att bara under­söka konver­gensen av generali­serade inte­graler.

Måndag 11/10

Jag blev litet sen med de här anteck­ningarna, eftersom jag hade ett möte med en ex­jobbare.

Jag gick igenom defini­tionen av Riemann-integral och tog ett exempel där vi skulle beräkna den tid det tar att för­flytta sig en viss sträcka, om hastig­heten var given i varje punkt på sträckan. Jag bevisade "Insättnings­formeln" och tog samma exempel igen, men nu genom att gå via deri­vator i stället för Riemann-summor. Jag tog också exemplet "konsument­överskott" (från national­ekonomin.) Sedan visade jag form­lerna för partiell inte­gration och variabel­substitu­tion. Det har vi ju tagit upp i samband med primitiva funk­tioner, men nu till­kommer ju att vi skall sätta in rätt gränser i inte­gralerna också. Jag hann med ett enkelt exempel på variabel­substitu­tion, men inget på partiell inte­gration.

Jag tog alltså inte upp några medel­värdes­satser, inte heller olik­heterna (fast de är ju rätt själv­klara.) Jag skall också vid något senare till­fälle ta upp beviset för Mac­laurins formel.

Onsdag 6/10

Jag skriver litet i förväg. Kapitel 5 är ganska om­fattande, och vi läser inte alla detaljer. Man skall naturligt­vis kunna inte­gralerna i utantill-listan. När det gäller rationella funktioner, så tar vi inte upp de besvär­ligaste fallen, och för inte­grander inne­hållande rot­uttryck kan vi också begränsa oss något. För trigono­metriska inte­grander använder man ofta ad-hoc-trix, och de måste vi ta upp i någon om­fattning, och även "tangens för halva vinkeln". Jag har skrivit en stencil om inte­graler som tar upp det här.

Nu finns inlämningsuppgift 2 Skall lämnas till lektionsläraren (sic! inte till mig) på lektionen den 27/10. Börja jobba med den redan nu!

Nu har jag haft föreläsningen, och den gick ungefär som jag planerat. Jag tog alltså upp trigonometriska integrander och rotuttryck, såsom jag behandlat dem i stencilen. Jag tog också upp ett par fall med uppdelning av partialbråk, eftersom de dök upp då jag räknade exempel, men jag har inte gjort något systematiskt om uppdelning i partialbråk! Det får lektionslärarna göra på fredag.

Fredag 1/10

Jag tog upp liet om konvexa och konkava funk­tioner igen; jag visade att geometriskt (vägt) medel­värde är mindre än mot­svarande arit­metiska medel­värde. Sedan definierade jag inflexions­punkt och tog ett enkelt tredje­grads­polynom som exempel.

Därefter började jag med primi­tiva funk­tioner. Här är en utantill-lista på bl.a. primi­tiva funk­tioner man bör lära sig utan­till. Jag introdu­cerade begreppet differen­tial, förs­ökte över­tyga att differen­tialen df(x)=f'(x)dx är en invariant (ut­trycket gäller även om x i sin tur är en funktion och dx följaktligen en differen­tial.)

Sedan började jag på kapitel 5; primi­tiva funk­tioner. Jag visade formeln för partiell inte­gration, och variabel­substitution. I det senare fallet uttryckte jag det så att vi söker en funktion vars differen­tial är f(x)dx, och att differen­tialens invarians innebär att mani­pula­tionerna i samband med variabel­bytet blir som de blir. Jag illu­strerade givetvis med några exempel både på partiell inte­gration och variabel­byte.

Det blev nog lika rörigt och obegripligt som beskriv­ningen ovan, så det är nog ingen dum idé att lektions­lärarna något tar upp dessa moment igen på lektions­under­visningen på måndag, även om jag formellt sett gått igenom det på före­läsningen idag. (Jag ursäktar mig något med att jag är förkyld och har huvudvärk.)

Måndag 27/9

Jag räknade exemplen 4.6a, 4.16, 4.12a (b lämnade jag som övning) genom att att göra tecken­scheman som i kapitel 4.3. Därefter tog jag upp konvexa (och konkava) funktioner (kapitel 4.6,) men jag vände litet på ordningen. Jag visade att för en funktion f(x) sådan att f''(x)>0 i ett inter­vall gäller att

1) grafen y = f(x) ligger ovanför varje tangent,

2) grafen y=f(x) ligger under varje korda.

Detta visade jag med hjälp av tecken­diagram. Sedan tog jag ett par exempel:

ln(x) =< x-1 för x>0, och

sin(x) > 2x/p för 0<x<p/2.

Slutligen visade jag "Jensens olikhet", ((14) sid. 242) för konvexa funktioner. Observera att jag hela tiden förut­sätter att f(x) är två gånger deriverbar, och att vi alltså tar andra­derivatans tecken som utgångs­punkt.

Glöm inte in­lämnings­uppgif­terna på onsdag!

Onsdag 22/9

Vi räknade exempel på Mack­laurin­utveck­lingar. Jag påpekade att när man vill Taylor­utveckla f(x) kring en punkt a, så är det oftast enklast att införa en ny variabel t = x-a och Mac­laurin-utveckla f(a+t). Vi utvecklade sin(x) kring x=p/6 på det sättet. Dessutom gjorde vi bl.a. uppgifterna 9.4, 9.21a, 9.34 och 9.36.

Tisdag 21/9

Jag pratade om Maclaurins formel och skrev upp ett par varianter av rest­termen. Vi väntar med det beviset tills vi läst integraler. Jag tog upp entydig­hets­satsen (se kap. 9.4 för beviset) och visade att man får Maclaurin-utveck­lingen av derivatan av f(x) genom att termvis derivera Maclaurin-utveck­lingen av f(x). Vi använde sedan dessa egenskalper för att bestämma Maclaurin-utvecklingen för ett antal elementära funktioner. Det här finns i kapitel nio i boken; se också den här stencilen. Här är en länk till en biografi om Maclaurin

Fredag 17/9

Första timmen var litet repetition och upphämtning. Jag skerv upp en lista på derivator man skall kunna utantill. Därefter räknade jag ett gränsvärde med L'Hôpitals regel, och använde produktsatsen för gränsvärden. Jag påpekade att det kan se ut som om man låter "ett x i taget" gå mot a, men att så får man inte göra generellt. Jag illustrerade med ett enkelt exempel. Alltså måste man se till att mam håller sig till räknereglerna. Jag skrev upp dem, och bevisade addirionssatsen för gränsvärden.

Andra timmen tog jag upp korollarier till medelvärdessatsen. Först L'Hôpitals regel (se stencilen), därefter att derivatans tecken visar om funktionen är växande eller avtagande i ett intervall. Jag illustrerade genom att visa olikheten (där jag slant iväg ett tag)

x/(1+x) < ln(1+x) < x      för x > -1

(med likhet för x=0)

Onsdag 15/9

Här är länkarna till stencilen om L'Hôpitals regel och biografin om Guillaume François Antoine Marquis de L'Hôpital som också finns i kursplaneringen.

Tisdag 14/9

Vi löste först problem 3.14. Sedan bevisade jag att deriver­bara funk­tioner är kontinu­erliga samt produkt­regeln och kedje­regeln för deri­vator.

Andra timmen skrev jag upp satserna (15), sid 149, och SATS 13 sid. 201. Dessa "bevisade" jag inte, utan vi tog dem som utgångs­punkt då vi gick igenom beviset för medel­värdes­satsen. Därefer skrev jag upp L'Hôpitals regel, och sa att beviset följer ur medel­värdes­satsen, och att beviset finns en stencil på nätet. I stället för att dra det, beräknade vi ett antal gräns­värden ur övnings­häftet kapitel 2 med hjälp av L'Hôpitals regel.

Jag gick alltså litet längre än jag skrivit i kurs­plane­ringen, så i princip kan ni ta upp exempel på L'Hôpitals regel redan i morgon, men det är nog bättre att öva mycket på deri­vation. Det är ju viktigt att man kan deri­vera med stor säker­het.

Måndag 13/9

Vi började på kapitel tre — deri­vator. Jag tog upp defini­tionen och här­ledde deri­vatorna för de elemen­tära funk­tionerna utom de cylko­metriska. Där­efter tog jag upp räkne­reglerna: summa, produkt, kvot och samman­sättning. Dessa bevisade jag inte; jag kommer att ta upp beviset för produkt och samman­sättning i morgon.

Sedan räknade jag ett antal exempel på framför allt deriva­tion av samman­sättning ("kedje­regeln".) Jag introdu­cerade då också implicit deri­vering, och deri­verade y(x)=x^x genom att deri­vera ln(y(x)) = x ln(x) implicit. Jag här­ledde sedan också deri­vatan för y(x) = arcsin(x) och y(x) = arctan(x) genom att deri­vera sin(y(x)) = x respek­tive tan(y(x)) = x implicit. Jag tog alltså inte upp deri­vatan av invers separat, utan gjorde mot­svarande med implicit deri­vering, vilket jag tror är lättare att göra rätt.

Inlämningsuppgift 1

Inlämnings­uppgifterna skall lämnas till lektions­lärarna på lektionen onsdagen den 29 september. Börja redan nu att arbeta med dem! Reglerna är: Ni får sam­arbeta, och det är OK att fråga lärare eller andra om detaljer. Men det är inte tillåtet att skriva av någon annans lösningar. Var och en skall alltså stå för sina egna lösningar, och vara beredd att redogöra för dem. Från oss lärares sida är syftet med inlämnings­uppgifterna att ni skall lära er matematiken, inte i första hand att det skall under­lätta tentamen.

Tänk på att lösningarna skall vara väl presenterade. Det gäller inte minst de två första uppgifterna.

Onsdag 8/9

Första före­läsningen var problem­lösning; vi räknade gräns­värden genom att använda våra "standard­gräns­värden". Andra timmen gick jag först igenom kapitel 2.5.4: serier. Jag tog upp defini­tionen, Sats 9 (geo­metriska serier), visade att den har­moniska serien diver­gerar och att S 1/k² konver­gerar genom att använda sats 10 och jäm­föra med serien i exempel 27.

Sedan gick jag igenom asymptoter och visade två exempel. Först en rationell funktion med en andra­gradare i täljaren och första­gradare i nämnaren. Den analy­serade vi genom att helt enkelt utföra divi­sionen. Sedan tog jag upp hyperbeln som finns i boken på sidan 163 (exempel 20.)

När det gäller kontinu­erliga funk­tioner har jag hittills bara tagit upp defini­tionen. "Satsen om mellan­liggande värden" osv. tar vi upp när det behövs i något samman­hang (som kan vara i något problem.)

Tisdag 7/9

Kapitel 2.1 och SATS 13 sid 114. Jag visade gränsvärdena (sin x)/x—>1 och (1-cos x)/x—>0 då x—>0.. Beviset i boken på sid 113–114 är ju fel! Det framgår ju inte alls att x < PT+TS som de skriver överst på sid 114! Jag gjorde på det vanliga sättet att jämföra areor. (Konstigt att dessa kompetenta författare gör en sådan tabbe!)

I samband med detta tog jag upp definitionen av gränsvärde (mitt på sidan 134) och visade att (sin x)/x—>1 verkligen uppfyllde villkoren i definitionen.

Därefter började jag med kapitel 2.3. Jag utgick från att gränsvärdet (1+x)^1/x då x—>0 existerar och definierade e som detta gränsvärde (formel (20) sid. 153.) Det är för långt och krångligt att ta kapitel 2.3 från början. Därefter härledde jag gränsvärdena (28) och (29). Slutligen visade jag gränsvärdet (32) med hjälp av Haralds lemma: jag tittade på ln för uttrycket, och visade att det går mot 0=ln(1).

Jag nämnde helt kort definitionen att f(x) är kontinuerlig; att det betyder att f(x)—>f(a) då —>a för alla a där f(a) är definierad. Jag sade att alla de elementära funktionerna är kontinuerliga, och det uppstod en viss diskussion om tan x verkligen är kontinuerlig, initierad av en klyftig fråga från en student.

Fredag 3/9

Här är några kommen­tarer (pdf.-fil) om inversa funktioner och de cyklo­metriska funktio­nerna.

Jag gick igenom cyklometriska funktionerna, men inte arccot; den bryr vi oss inte om! Vi tittade på graferna för y= arcsin(sin x) y = sin(arcsin x), y = arctan(tan x) och y = tan(arctan x). En del av dessa lämnade jag som övning att verifiera. Jag visade att arccos x = p/2 - arcsin x och att arctan(1/2) + arctan(1/3) = p/4.

Sedan visade jag ganska snabbt att exopnenter växer snabbare än potenser, och att logaritmer växer långsammare än potenser då x växer mot oändligheten; dvs a^x/x^b—>oändl. och ln(x)/x^b—>0 då x—>oändl., förutsatt att a>1 och b>0.

Nästa vecka fortsätter vi med gränsvärden.

Måndag 30/8

Jag pratade om summasymbolen och visade att man kan skifta index i en summa (användbart ibland.) Jag härledde formeln för geometrisk summa, däremot inte aritmetrisk summa, och tog upp teleskoperande summor. Exempel:

1 + 3 + 5 + ... + 2n-1 = n²

Det ser vi genom att skriva 2k-1 som k² - (k-1)².

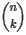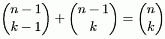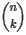Jag skrev upp Pascals triangel, som man får genom att i en rad addera talen snett ovanför. Sedan definierade jag binomial­koeffici­enterna enligt (13) i kap.1 i boken och visade egen­skapen . Härur visade jag med ett informellt induktions­resonemang att talen i Pascals triangel är just binomial­koeffici­enterna. Sedan använde jag ett liknande informellt induktions­resonemang för att visa att är antalet sätt att plocka ut k element bland n utan hänsyn till ordning. Slutligen tog jag exemplet med rut­nätet som skall täckas med L-klotsar som ytter­ligare ett informellt exempel på inuktions­resonemang.

Jag hann alltså inte med binomial­satsen! Jag hoppas att lektions­lärarna tar upp det på lektionen på onsdag. Det är ju nu ganska lätt att göra precis som det står i boken på sidan 62.