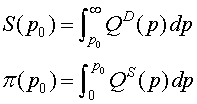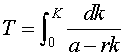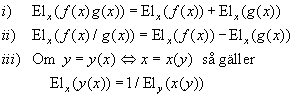Kursens hemsida
Aktuell Information

Tentan är rättad

men resultatet kommer inte in i LADOK förrän tidigast på måndag 27/2 eftersom Claudette har semester.

Tentorna finns på studentexpeditionen.

Resultat: A: 0 st, B: 6 st, C:13 st, D: 11 st, E:20 st; FX: 0 st, F: 40 st.

Slutbetyget bestäms av följande enkla regel. Låt 0 representera E, o.s.v. 4 representera A. Tag 0.24*(TenA)+0.76*(TenB) där (TenA) och (TenB) är motsvarande siffer­betyg. Runda av till närmaste heltal, gå tillbaks till bokstavs­betyg.

Svar till tentan 11/2/2012

Svaret på uppgift 2 är nu korrigerat.

1. 6.59% per år med kontinuerlig förräntning, 6.82% med årlig förräntning,

2. 82'926.62

3. 4

4a. p=2.4938, Q=1.4752

4b. 3.9600

4c. 0.07527

5. 1.99317. (”exakt” värde är 1.99315)

6. Se läroboken.

Anmälan till omtentamen TEN B 11/2/2012

skall göras på ”mina sidor” 16/1–30/1 2012.

Omtentan på del 1

är litet försenad p.g.a. att Johan har haft lung­inflammation. Jag räknar med att den skall vara rättad måndag eller tisdag 21–22/11.

Tentan är rättad.

Finns på studentexpeditionen.

Resultat: 112 skrivande, 11 godkända (alltså knappt 10%.)

Bedömning: Varje uppgift gav max. 6 poäng, totalt kan man alltså få 36p.

           33–36p: A
           29–32p: B  (1)
           25–28p: C  (0)
           21–24p: D  (2)
           17–20p: E  (8)
              16p: FX (0)
             ≤15p: F (101)

Medianvärdet var 5p (dvs fler än hälften hade ≤5p, fler än hälften hade ≥5p). Typvärdet (det vanligaste resultatet) var 2p.

Tentan 18/10/2011 med svar

Lokaler för tentan 18/10/2011

           Ab-Bö V01
           Ca-He V11
           Hj-Le V22
           Li-St V32
           Sv-Öb V34
           Extra (ej anmälda) E31

Jag har mottagning måndag 17/10 10:00 – 16:00.

Jag finns på mitt rum, eller däromkring. Gå in genom nedre dörren vid ute-trappan under tak som går från Klocktornet. Dörren skall vara upplåst mellan kl.10 och 16.

Omtentan på del 1

kommer att äga rum torsdagen 27/10 kl. 13:30–15:30. Vi meddelar lokal(er) senare.

Torsdag 13/10

Det blir litet blandade exempel, utan sammanhang.

Onsdag 12/10

Vi studerade först funktionen y = y(x) given genom sam­bandet

xy³ – x³y = 2x. Vi bestämde andra ordningens approxi­mation till y(x) för x ≈ 1

Därefter visade jag ett par olikheter med hjälp av tecken­studier av detivata och andra­derivata.

Slutligen gjorde vi en andra ordningens approxi­mation av en funktion i när­heten av noll, fast där blev uttrycket 0/0. Vi gick då tillbaks till här­ledningen av uttrycket, som var en summa, och paniken försvann.

Sista övningen i morgon torsdag: Repetera och hämta upp. Jag ger inga specifika nya uppgifter.

Tisdag 11/10

Först pratade jag litet om duration när man har kontinuerlig förräntning, alltså diskonterings­faktor e^–r⋅t. Vi räknade dels med diskreta betalströmmar, dels med kontinuerliga.

Därefter tog jag ett exempel på konsument­överskott, producent­överskott och välfärd. Vi införde en skatt på den vara vi studerade och fann att en del välfärd försvann, den tillföll varken producenten, konsumenterna eller staten. Dead Weight Loss, som det kallas.

Måndag 10/10

Jag visade först Shepards lemma (example 3 sid 516).

Observera metoden: jag gör så här (kopiera på övningarna)

Jag skriver C = C(K,L,r,w) = rK + wL,   Q = F(K,L).

FOC (”First Order Conditions”)

C_K = λF_K

C_L = λF_L

I optimum får vi C*(r,w,Q) = C(K*(r,w,Q), L*(r,w,Q),r,w).

dvs. om vi differentierar och använder FOC:

dC* = C_KdK* + C_L dL* + C_rdr + C_wdw

dC* = λ(F_K dK* + F_L dL*) + C_r dr + C_w dw

dC* = λ dQ* + K* dr + L* dw

Alltså ∂C*/∂ r = K* o.s.v.

Därefter var det lätt att lösa problem 14.7:6.

Sedan tog jag upp nuvärden av kontinuerliga betalströmmar, då räntan gottgörs kontinuerligt. Formel (5) sid. 3.5.5. Vi har gjort detta tidigare, men jag repeterade och gjorde en litet annorlunda härledning eftersom det varit en del frågor om detta.

Här är övningar ni kan använda på onsdag.

Torsdag 6/10

Jag löste uppgift 3 på tentan 22/10/2010 och uppgift 6 på tentan 10/1/2011.

Därefter uppgifter ur boken: 13.7: 1b, 3. I samband med den sista uppgiften härledde jag Hotellings Lemma.

På övningen i morgon kan ni gärna göra uppgift 6 på sidan 4 (4. Fler övningar) i övnings-pdf-en och övningarna 5 och 6 på sidan 6 (6. Lagranges Multiplikator­metod.)

Onsdag 5/10

Jag ägnade dagen åt två problem.

Först studerade vi Markowitz' portfölj­problem där vi hade möjlighet att inverstera i tre finansiella till­gångar

i) En stats­obligation som ger säker av­kastning på 3%. (Det är alltå inte fråga om Grekiska eller Italienska stats­obligationer, utan t.ex. Svenska.)

ii) En ”aktie” A som ger förväntad av­kastning 7% med en volatilitet på 20%,

iii) En ”aktie” B som ger förväntad av­kastning 9% med en volatilitet på 28.28%. Vi löste bl.a. problemet att bestämma den portfölj som ger högst förväntad av­kastning, givet att dess volatilitet är högst 15%.

Därefter löste jag problem 14.7:4 i boken.

Måndag 3/10

Jag ägnade hela föreläsningen åt två problem. Först uppgift 4 på tentan 23/8/2011. Denna uppgift löste jag på flera olika sätt, dels med ”analytiska” metoder, dels med numeriska.

Därefter ”konsumentteori”. En konsument maximerar sin netto-nytta

C(x,p) = V(x) – px

över x. Vi beräknade efter­fråge­funktionen, konsument­över­skottet m.m. i ett konkret fall och fann att konsument­över­skottet blev detsamma som den maximerade netto­nyttan.

Därefter visade jag att denna sista observation gäller helt generellt.

Jag ställer in föreläsningen tisdag 4/10 kl. 8–10.

I stället har jag mottagning måndagen den 17/10 klockan 10-16 (dagen före tentan) då ni kan komma med frågor. Jag återkommer om lokal!

Här är övningsuppgifter ni kan använda till övningen på onsdag.

Torsdag 29/9

Förmiddagen ägnade vi åt ett enda problem: Givet en kupongobligation med givna utdelningar och nollkupongräntor som varierar med löptiden

a) Beräkna nuvärdet

b) Beräkna ”yielden” (avkastningsräntan (?))

c) Beräkna (modifierade) durationen.

Vi gjorde detta genom att använda finessen med listor på miniräknaren. Jag definierade också begreppet (modifierad) duration, och förklarade hur den beskriver obligationens känslighet för förändringar i ränta.

Eftermiddagens föreläsning ställer vi in. Dels för att det blir för mycket för er studenter (14 timmar denna vecka varav åtta timmar onsdag-torsdag är för mycket); räkna själva i stället! men också för min skull (mår dåligt efter en matförgiftning.)

Övningen i morgon. Nu kan ni göra alla uppgifter på övnings-pdf-en. Vi har gått igenom allting. Ni bör ha uppgifter kvar att göra, och för framtiden skall jag producera fler.

Onsdag 28/9

Skriver i förväg. Jag tar upp ytterligare några exempel. Eventuellt visar jag Shepards Lemma. Övningslärare: observera att jag inte använt bokens beteckningar med ”Lagrange­funktion”. I stället har skrivit ekvationerna som

f '_x(x,y) = λ g'_x(x,y)

f '_y(x,y) = λ g'_y(x,y)

med lätt insedda beteckningar.

Tisdag 27/9

Igår satte jag betygen på första deltentan. Jag tror resultaten finns i LADOK nu, så ni kan de dem i ”Mina Sidor”. Tenrorna finns på student­expeditionen.

Betygsgränser. Varje uppgift ger max. 6p. För att bli godkänd ö.h.t. skall man ha ≥4p på första uppgiften och ≥6p på de övriga. Därefter

10–14p: E, 14–17p: D, 18–22p: C, 23–26p: B, 27–30p: A.

Resultat: 58 F, 19 E, 26 D, 20 C, 5 B, 0 A.

Jag skriver detta innan jag har föreläsningen. Jag skall nu börja med kapitel 14, metiden med Lagrange-multiplikatorer. Jag planerar att gå igenom example 1 sid 499, därefter en variant av example 3 sid. 492 där jag också kommer att visa att lagrange-multiplikatorn blir derivatan av målfunktionen m.a.p. m, d.v.s ett konkter fall av ”envelope-satsen” (varianten kapitel 14.2). Jag tar ockå upp ett eget påhittat exempel.

På övningen i morgon kan ni alltså ta upp följande problem:

uppgift 7 på tentan 23/8/2011 (finns på stencilen med övningar)

uppgift 4 på tentan 10/1/2011

uppgift 5 på tentan 22/10/2010

Alla uppgifter på sidan 6 i pdf-en med övningar.

Det hinner ni givetvis inte med, så det blir över till kommande övningar.

Torsdag 22/9 och fredag 23/9

Jag har nu gått igenom kalitel 13, max- och min-problem. Inte metoden med Lagranges multiplikatorer, det kommer i kapitel 14.

Observera att vi inte tar upp några metoder för att bestämma karaktären hos en stationär punkt. Det blir alldeles för svårt så snart vi har mer än två variabler.

Förutom några exempel jag hittat på själv har vi tittat på example 3, sid 455, men i stället för Cobb-Douglas-specifikationen i example 4 tog jag följande konkreta exempel:

F(K,L) = K – 0.1K² + L – 0.1L² + 0.1 KL Här skrev vi upp ”första ordningens villkor” som vi differentierade och fick

–0.2 dK + 0.1 dL = (1/p) dr

0.1 dK – 0.2 dL = (1/p) dw

Vi löste detta system och fick

dK = –(10/3p) dw – (20/3p) dr

dL = –(20/3p) dw – (10/3p) dr

Ur detta ser vi vad alla fyra partiella derivatorna (∂K/∂w o.s.v.) är. Vi konstaterade att om räntan är högre (dr > 0) så minskar K, inte förvånande, men även arbetskraften L minskar. Det tror vi beror på termen 0.1 KL i produktions­funktionen: arbets­kraftens marginal­produkt ökar med mängden kapital K.

Detta är ett exempel på komparativ statik.

Vi har också studerat problem 13.2:7 och 13.2:2 och 13.3:2. I den sista uppgiften visade jag, med ad-hoc-metoder att (0,0) är ett lokalt minimum, men inte ett globalt De två övriga stationära punkterna, (–1, –1) och (–1, 1) såg vi var varken globala max- eller minpunkter, men vi gjorde ingen lokal analys (observera att vi inte tar upp sådana metoder i den här kursen!).

På övningen på måndag kan ni alltså ta upp övningarna under punkt 9 i kursplanen. Ni kan strunta i d)-uppgiften i 13.4:5.

Onsdag 21/9

Förmiddag. Jag utgick från övning 11.6:1 för att repetera partiella derivator, linjär aproximation och differentialer vi såg t.ex. att den linjära approxima­tionen blev bättre ju mindre vi gjorde inkrementen.

Därefter använde jag exempel 1 kap. 11.7 för att definiera och förklara begreppen ”marginal­produkt” och ”marginell substitutions­kvot”. Det senare begreppet dyker inte upp i boken förrän i kapitel 12.5, men jag tycker det är lämpligt att ta upp det i det här samman­hanget.

Vi använde bokens exempel med Cobb-Dopuglas som konkret illustration.

Eftermiddag. Repeterade delar av kapitel 10. Först härledde jag rigoröst att om räntan ρ förräntas kontinuerligt, så är diskonterings­faktorn (för nuvärden) exp(-ρt). Därefter härledde jag rigoröst formeln (5) sidan 355 (med litet andra beteckningar).

Därefter beräknade vi nu­värdet av en betal­ström med given (kontinuerlig) ränta numeriskt på miniräknaren. Sedan tänkte vi oss att samma betal­ström i stället var utfallet av en initial investering, och beräknade intern­räntan för denna investering; även detta med miniräknaren.

Slutligen gorde vi ett liknande exempel då betalningarna kom halvårsvis.

På övningen i morgon fortsätter ni alltså med de uppgifter ni redan fått fram till och med kapitel 12.

Måndag 19/9

Jag planerar att gå igenom kedjeregeln i flera variabler, differentialer, och differentialens invarians (kap. 12.9).

När det gäller kedjeregeln, så beskriver jag den som att man deriverar m.a.p. en plats i taget och adderar. Exempel: antag att vi skall derivera F(x(s,t,u), y(s,t,u)) m.a.p. t. Vi har då t på två ställen i detta uttryck. Om jag nu deriverar m.a.p det första t:et och struntar i att det andra finns, så får jag

F_x(x,y)⋅x_t.

Nu gör jag samma sak med det andra t:et: jag deriverar m.a.p. detta och struntar i att det första finns. Då får jag

F_y(x,y)⋅y_t. Den partiella derivatan av F(x(s,t,u), y(s,t,u)) m..a.p. t är nu summan av dessa:

∂F/∂t = F_x(x,y)⋅x_t + F_y(x,y)⋅y_t.

Jag tror att denna operationella beskrivning är enklare att använda än formeln för kedjeregeln. Dessutom ser vi att t.ex. derivatan av en produkt en en variabel är ett specialfall: Låt oss derivera f(x)g(x). Vi derivera m.a.p. ”första” x:et och bertaktar det andra som en konstant. Det ger

f '(x)g(x)

Sedan deriverar vi m.a.p. ”andra” x:et och bertaktar det första som en konstant:

f (x)g' (x)

och när vi summerar får vi derivatan av en produkt: d(f(x)g(x))/dx = f '(x)g(x) + f(x)g'(x). ”Produktregeln” är alltså ett specielfall av ”kedjeregeln” i flera variabler.

Angående övningen i morgon. Välj bland de övningar i boken som finns listade under punkt 8 i kursplanen. Naturligtvis hinner ni inte med tillnärmelsevis alla dessa. Välj ut några ur varje typ, och sedan får studentera fixa resten hemma. Var beredd på frågor!

Fredag 16/9

Jag avslutade kapitel 10 igår. Detta är naturligtvis ett viktigt kapitel i denna kurs.

Idag började jag med funktioner i flera variabler. Kapitel 11.1 0ch 11.2, fast generaliserat till funktioner även med fler än två variabler. I stället för en formell definition av partiell derivata besktev jag linjär approximation:

Δf(x,y,z) ≈ f_x(x,y,z)Δx + f_y(x,y,z)Δy + f_z(x,y,z)Δz

och omvänt; om

Δf(x,y,z) ≈ A Δx + B Δy + C Δz

så gäller A = f_x(x,y,z), o.s.v. Litet vagt, onekligen, men det får duga.

Sedan tog jag upp partiella elasticiteter, kapitel 11.8, och förklarade att dessa kan tolkas via approximationen

Δf/f ≈ El_x(f) Δx/x + El_y(f) Δy/y + El_z(f) Δz/z.

Sedan andra ordningens derivator, och att blandade derivator är lika (derivatan m.a.p. först x, sedan y är densamma som först y, sedan x.)

Torsdag 15/9

Detta skriver jag i förväg, för övningarnas skull.

Jag planerar att ta upp amorteringar (kapitel 10.6) samt formlerna för kontinuerlig förräntning (undre formeln (1) sid. 346 och formel (5) sid 355). I det samman­hanget visar jag också hur man integrerar numeriskt med TI:s miniräknare.

På övningen kan ni ta upp följande uppgifter ur boken:

Review Problems 1–4 i kapitel 3 i den utsträckning det behövs. De kan också öva på att beräkna summorna med mini­räknarens sum(seq(formel(x),x,n,m,1)).

Problemen 10.5: 1–3 ; observera att 3,ii) är felaktigt formulerad!. Det skall stå att första ut­betalningen sker om ett år (den sista alltså om 10 år).

Problemen 10.5: 4, 8

I samtliga fall kan man lösa problemet analytiskt eller numeriskt på mini­räknaren.

Problem 10.6: 1, 3; 10.7: 1 (lös numeriskt!), 7 (lös numeriskt!).

Onsdag 14/9

Jag började på kapitel 10. Men först tog jag upp summa-symbolen i kapitel 3. Jag härledde formeln för en geometrisk summa (den tredje inramade formeln under punkt 5 i undervisnings­planen, som finns på kursens web­sida). Därefter definierade jag nuvärdet av ett framtida kassaflöde c_t vid tiden t (”nu” är tiden 0) som

PV = c_t(1+r)^-t

d.v.s. den övre av formlerna (1) på sidan 346. Därefter definierade jag nuvärdet av ett periodiskt kassa­flöde enligt formel (1) på sidan 352.

Sedan kombinerade vi med geometriska summor, och härledde formel (2), sidan 353.

Jag nämnde också att om räntan med olika löp­tider är olika (termins­strukturen är inte platt) så beräknas nuvärdet genom

PV = Σc_k(1+r_k)^-k

och då definieras avkastningsräntan (”yield”) r som lösningen r till ekvationen

PV = Σc_k(1+r)^-k

och på motsvarande sätt internräntan: om man investerar ett belopp PV vid tiden 0 och sedan får betal­strömmarna c_k vid tiderna k, så kallas lösningen till ekvationen ovan ”intern­räntan” för denna investering.

Jag visade slutligen dels hur man kan numeriskt beräkna summor på TI:s miniräknare, och också hur man numeriskt löser ekvationer som den ovan. Vi tittade på ett konkret exempel.

Jag har alltså hoppat omkring litet i kapitel 10, och jag har inte ännu tagit upp annat än periodisk (t.ex. årlig) förräntning.

Lokaler till tentan idag 13/9.

För er som är anmälda gäller förjande salar; efternamn:

          A-En     V23
          Eo-Ho    V33
          Hp-La    V34
          Lb-Pe    V35
          Pf-Sto   Q11
          Stp-Öö   Q21

För er som inte är anmälda: Det finns några extra platser i V33 och V34. Pröva om ni får plats där.

Måndag 12/9

Vi repeterade bara. I morgon är första tentan, och övningslärarna kan gå igenom den på övningen på onsdag; det bli väl allt som händer då.

Min kollega Gunnar Englund kommer att besöka salarna för att svara på eventuella frågor; jag skall ta hand om lille August.

Jag har fått påpekat för mig att det var fel i svaret i övningarna, senaste tentan, augusti 2011, uppgift 6. Det är korrigerat nu.

Torsdag 8/9

Jag gick igenom konsument­överskott och producent­överskott, men med direkt efterfrågan respektive utbud. Vi har alltså formlerna

där p₀ är priset. Övre formeln (konsument­över­skottet) gäller om p₀ ≥ jämvikts­priset, vilket är det normala, medan undre formeln (producent­överskottet, vinsten) gäller om p₀ ≤ jämvikts­priset.

Därefter började vi med litet repetition: jag tog två uppgifter på maximum, minimum, konvexitet och konkavitet. På måndag blir det bara repetition.

Onsdag 7/9

Integraler, kapitel 9.1, 9.2, 9.4. Jag ”visade” area-representationen för integraler, och påpekade m.h.a. några exempel att ”area” kan betyda konor, år eller något annat; dvs ”arean” har dimensionen x⋅y.

Jag visade sedan att om man lånar K kronor till räntan r (kontinuerlig förräntning) och amorterar a kronor per tidsenhet (kontinuerligt) så är den tid det ar innan lånet är betalat

och denna integral kunde vi beräkna. Jag tog också ett exempel där man kör bil med en hastighet som varierar med sträckan. Även i detta fall blev tiden det tar att komma fram en integral: integralen av 1/hastigheten m.a.p. sträckan från noll till avståndet till destina­tionen. I bägge dessa fall kan tiden represen­teras av en ”area”.

I morgon tar jag upp konsument­överskott och producent­överskott, men jag integrerar den ”direkta” efter­frågan, inte den inversa, som boken gör.

Tisdag 6/9

Jag tog upp begrepet ”marginal-” som ofta förekommer i språk­bruket i ekonomi: ”marginal­skatt”, ”marginal­kostnad”, ”marginella konsumtions­benägenheten” o.s.v. och påpekade att det matematiska begreppet är en derivata.

Sedan tog jag upp max.- och min.-problem då funktionen är konvex eller konkav, d.v.s. derivatan = 0 => min.-punkt eller max.-punkt beroende på om funktionen är konvex eller konkav i intervallet. Jag hann bara med två enkla exempel.

Därefter fortsatte jag med example 3 sid 266–267, fast jag gjorde litet mer av exemplet än boken. Jag visade att en ”marginell” ökning av ”marginal­kostnaden” innebär en pris­ökning som är halva kostnads­ökningen om efterfrågan är linjär, men hela kostnads­ökningen om efterfrågan är exponentiell: x(p) = a⋅exp(-θ p).

Måndag 5/9

Jag tog upp begreppet ”elasticitet” som står i kalitel 7.7. Jag visade följade räkne­regler för elasticiteter som ni bör lära er ”utantill”

Jag tog också upp ett exempel från mikro­ekonomi, example 3 sid 266–267, fast jag gjorde en litet annan analys där räkneregeln iii) kom till användning.

I morgon skall jag bl.a. fortsätta med detta exempel.

Om miniräknare på tentorna.

Det finns ju formel­manipulerande ”mini­räknare” (TI89), som jag hade tänkt att inte betrakta som ”mini­räknare” (utan som liten dator).

Nu har jag blivit varse att någon idiot på skol­verket bestämt att även sådana räknare tillåts i skolan vid prov där mini­räknare är tillåtet hjälp­medel.

Det är enklast om vi gör som i skolan, så slipper vi dessutom problem med att skrivvakter måste kontrollera vilken modell av räknare ni har. Det innebär att på första tentan (3p) är inga mini­räknare tillåtna, medan på andra tentan alla mini­räknare är tillåtna hjälpmedel.

Torsdag 1/9

Jag gick igenom linjär och kvadratisk approxi­mation. Linjär approxi­mation står i kapitel 7.4, kvadratisk approxi­mation i kapitel 7.5. Vi tar bara upp mot­svarande formel (1) sid 216 och formel (2) sid 221; vi gör alltså inga högre ordningars approxi­mationer, och inget om feltermer.

Jag räknade ett par exempel, bl.a. uppgift 5 på sidan 224.

Mot slutet tog jag också upp en ekonomisk tillämpning, men det var knappt om tid, så det gick ganska snabbt.

På övningen i morgon kan ni fort­sätta med det ni höll på med vid förra övningen, och sedan fortsätta med ”andra ordningens derivator”, ”Växande, avtagande”, ”Konvexitet, konkavitet”.

Om detta inte räcker kan ni leta fram flera sådana upp­gifter senare i övnings­häftet, t.ex. ”3. Blandade övningar” nr 4 och 5, ”5. Ännu fler övningar” nr. 8, ”Repetitions­uppgifter” nr. 9, Tentan 10/1/2011 nr. 2 och 5, tentan 23/8/2011 nr. 5.

Om inte detta räcker finns ju också övningar i boken; se kursplanen.

Onsdag 31/8

Jag gick igenom växande och avtagande funktioner (kap. 6.3), konvexa och konkava funktioner (kap. 6.9) och implicit derivering (kap. 7.1).

Tisdag 30/8

Jag skrev upp en del räknelagar för potenser, logaritmer och derivator. Den svåra deriverings­regeln är den för samman­satta funktioner (”kedje­regeln”), så jag tog upp den igen, skrev den på en litet annan form och demonstrerade med ett par exempel. Sedan tog jag upp ”logaritmisk derivering” (som är ett exempel på ”implicit derivering”). Sedan fick ni pröva på att själva derivera några uttryck, och de sista minutrarna gick jag igenom ett par av dessa uppgifter.

Måndag 29/8

Efter en genomgång av administrativa detaljer började vi med matematiken. Jag gav ett antal uppgifter på att ”förenkla uttryck” av typen 1.1–1.6 i övningrna. Efter att ni prövat på dem en stund gjorde jag dem på tavlan. Andra timmen ägnade vi åt deriverings­reglerna: produkt, kvot och samman­sättning. Vi gjorde likadant: ni prövade på ett par uppgifter av var sort, och sedan gjorde jag dem på tavlan. Uppgifterna var av samma typ som under ”2. Derivator” fram till ”Logaritmisk derivering” i övningrna.

Logaritm­lagarna finns på sidan 121 i boken. Vi härledde också den användbara identiteten

a^x = e^x⋅ln(a).

Räknelagar för exponential­funktioner och potenser står inte explicit i boken; ni får konsultera era gamla gymnasieböcker om ni är osäkra.

Räknereglerna för derivator står i kapitel 6.7, 6.8.

De här sakerna skall ni kunna ”utantill”.