The rate of change of the osculating
plane of a space curve. The
torsion 
is positive for a
right-handed curve, and negative for a
left-handed curve. A curve with curvature 
is planar iff 
.
The torsion can be defined by
 |
(1) |
where N is the unit normal vector and B is the unit binormal vector. Written explicitly in terms of a parameterized vector function x,
 |
 |
 |
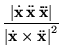(2) |
|
 |
(3) |
(Gray 1997, p. 192), where
denotes
a scalar
triple product and 
is the radius of
curvature.
The quantity 
is called the radius of
torsion and is denoted 
or
.
Bundle Torsion,
Curvature, Group Torsion,
Radius of
Curvature, Radius of
Torsion, Torsion Number,
Torsion
Tensor
Gray, A. "Drawing Space Curves with Assigned Curvature." §10.2 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 222-224, 1997.
Kreyszig, E. "Torsion." §14 in Differential Geometry. New York: Dover, pp. 37-40, 1991.
 | |||
 |
|
| |