1.  H. Anton and C. Rorres, Elementary Linear Algebra, Applications Version. ISBN: 0-471-30570-7. Säljes på THS Bokhandel.

2.   Kurt Johansson och Henrik Shahgholian, Kompletteringskompendium till kursen Linjär algebra, Institutionen för matematik, KTH. Säljes på matematiks elevexpedition.

1.1
Det viktigaste här är övergången mellan två sätt att beskriva ett linjärt ekvationssystem:
Det vanliga, med variabler utskrivna:

och matrisversionen där variablernas koefficienter samt de konstanta högerleden bildar systemets totalmatris (=augmented matrix):

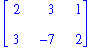
Som inledning till Gauss-eliminationen i nästa avsnitt bör man också lära sig de elementära radoperationerna.

Satser och begrepp: Linjärt ekvationssystem, totalmatris (Augmented matrix), elementära radoperationer.

Hemuppgifter: 1def, 2, 4cd, 8, 5bd, 12.

1.2
Här finns fyra viktiga begrepp som hör ihop parvis: Med Gauss-elimination reducerar man systemets totalmatris till trappstegsform. Och med Gauss-Jordan-elimination reducerar man totalmatrisen till reducerad trappstegsform.

Gauss-Jordan-elimination drivs alltså längre än Gauss-elimination. Vid Gauss-elimination avslutas systemets lösning med s.k. återsubstitution (back-substitution).
Dessa fyra begrepp är viktiga. De två eliminationsmetoderna måste tränas in med ett lämpligt antal hemuppgifter.

Notera också de tre tänkbara fallen vad det gäller antal lösningar till ett linjärt ekvationssystem: En unik lösning, oändligt många lösningar eller ingen lösning alls.

Observera att i det homogena fallet (då alla högerled är 0) finns det alltid en lösning, den triviala (då alla variabler får värdet 0). Man får alltså då endast två fall: En unik lösning (den triviala) eller oändligt många.

Satser och begrepp: Reducerad trappstegsform (Reduced row-echelon form), trappstegsform (Row-echelon form), Gauss-Jordan-elimination, Gauss-elimination, återsubstitution (Back-substitution), homogent system (Homogeneous system).

Hemuppgifter: 1, 2, 3aef, 4ab, 5d, 6a, 7cd, 8c, 10b, 13b, 14b.

1.3
I detta avsnitt studerar man matriser och deras operationer. Notera att man kan skriva ett linjärt ekvationssystem på den enkla formen: Av = b, där A är någon matris som kallas systemmatrisen till systemet samt v och b två vektorer varav v har variablerna och b högerledskonstanterna som komponenter.

Av matrisoperationerna är multiplikation mellan matriser den som fordrar en del övning. Notera att matrisernas dimensioner måste passa ihop för att multiplikation skall vara möjlig. Närmare bestämt: I produkten AB måste A:s radantal vara lika med B:s kolumnantal.

Lär dig också om transponat (transpose) som skrivs A^T och betyder att A:s rader och kolumner byter plats.

Begreppet spår (trace) ingår också i avsnittet. Spåret av A, tr(A), är lika med summan av A:s diagonalelement.

Satser och begrepp: Matris och element (matrix and entry), matrisaddition, multiplikation med skalär, matrismultiplikation, transponat (transpose), spår (trace).

Hemuppgifter: 1abcdh, 3bgjk, 4a, 5cg, 6acd, 13b, 14b.

1.4
Avsnittet börjar med en genomgång av reglerna för matrisaritmetik (Theorem 1.4.1.): de flesta regler som gäller för reella tal också gäller för matriser. Observera dock det viktiga undantaget: AB = BA gäller inte allmänt för matriser.

Här definieras också det viktiga begreppet inversmatris (Inverse Matrix): Matrisen A^-1 är inversen till matrisen A om AA^-1 = A^-1A = I, där I är den enhetsmatris (med ettor i huvuddiagonalen och nollor i övrigt). Detta begrepp är tillämpligt på kvadratiska matriser. Inte alla kvadratiska matriser har en invers. Men om A har en invers, A^-1, så är inversen unik (Theorem 1.4.4.).

I Theorem 1.4.5. anges formeln för inversmatrisen A^-1 till den allmänna 2x2-matrisen A.

Notera i övrigt särskilt de snarlika relationerna: (AB)^-1 = B^-1A^-1 (Theorem 1.4.6.) och (AB)^T = B^TA^T (Theorem 1.4.9.)

Satser och begrepp: Matrislagar s.38, nollmatris s.40, identitetsmatris s.41, inversmatris s.42, 2x2-matrisens invers s.43, matrispotenser (powers of a matrix) s.44-45, regler för transponatmatriser s.46-47.

Hemuppgifter: 3d, 4B, 5, 7b, 12, 14, 15.

1.5
Avsnittet introducerar begreppet elementär matris. Grundidén är, Theorem 1.5.1, att en elementär radoperation som transformerar en totalmatris A till en ny totalmatris B kan representeras av en matris E så att B = EA (notera att A multipliceras med E från vänster).

Detta ger en metod att bestämma A^-1:

1.  Placera matrisen A till vänster och enhetsmatrisen I till höger (separerade av en streckad linje) i en utvidgad totalmatris.
2.  Utför sedan de elementära radoperationer som transformerar vänstermatrisen A till I och applicera samtidigt dessa operationer på högermatrisen.
3.  När vänstermatrisen är färdigtransformerad till I, har högermatrisen transformerats till den sökta inversmatrisen A^-1.

Satser och begrepp: Elementär matris s. 50, Metoden att bestämma inversmatriser, (Example 4) s. 55.

Hemuppgifter: 1, 3b, 5a, 6d, 7bd, 9ab.

1.6
I detta avsnitt formuleras en del viktiga fakta om linjära ekvationssystem. Först formuleras satsen om de tre fallen som kan uppstå vad gäller antalet lösningar till ett linjärt system: ingen lösning, en lösning eller oändligt många lösningar (Theorem 1.6.1 s. 59).

Theorem 1.6.2 utsäger att om A är inverterbar så har det linjära systemet Ax = b lösningen x = A^-1b.

Theorem 1.6.4 formulerar en rad ekvivalenta villkor som alla representerar fallet med en unik lösning till Ax = b där A är kvadratisk. Att ekvationssystemet har en unik lösning är bl.a. ekvivalent med att A är inverterbar.

I detta avsnitt visas också hur man kan lösa flera system på en gång om dessa har samma systemmatris (Example 2 s. 61).

I Example 3 s. 63 diskuteras slutligen hur man kan finna villkor på högerleden som säkerställer att systemet har någon lösning.

Satser och begrepp: Thm 1.6.1-4, Ex. 2, Ex. 3.

Hemuppgifter: 2, 4, 8, 12, 13, 18.

1.7
Avsnittet tar upp diagonala matriser, triangulära (över- och undertriangulära) samt symmetriska matriser.

De triangulära matrisernas egenskaper finns listade i Theorem 1.7.1, bl.a: Triangulära matriser behåller sin form vid invertering och vid multiplikation med en annan matris av samma form.

Några egenskaper hos de symmetriska matriser finns samlade i Theorem 1.7.2 och 1.7.3.

Satser och begrepp: Diagonal matris s.66, triangulär matris (samt över- och undertriangulär) s.68, symmetrisk matris s.70.

Hemuppgifter: 2a, 3b, 4, 9, 13, 15a.

2.1.
Här definieras determinanten för en kvadratisk matris A, det(A).

Talet det(A) definieras som en summa av elementära produkter av A:s element där tecknet framför varje produkt bestäms av vilken sorts permutation (jämn (ger +) eller udda (ger -)) produkten svarar mot. Dessa begrepp förklaras närmare på s. 81-83.

I Figure 2 nederst på s. 83 ges en sorts grafiska metoder för beräkning av determinanter för 2x2- och 3x3-matriser.

 Satser och begrepp: Permutation och elementär produkt s.80-81, determinant s.81.

Hemuppgifter: 4, 7, 8, 10, 18.

2.2. I Thm 2.2.1-2.2.2 ges några användbara determinantegenskaper:
(a) Om A har en nollrad så är det(A) = 0.
(b) det(A) = det(A^T).
(c) Om A är en trappstegsmatris, är det(A) = produkten av diagonalelementen.

Thm 2.2.3 och 2.2.4 utgör en utredning av hur de olika radoperationerna i Gauss-eliminationen påverkar matrisernas determinanter:
(a) En rad (eller kolumn) multipliceras med k : det(A) -> k^.det(A)
(b) Två rader (eller kolumner) byter plats : det(A) -> -det(A)
(c) Två olika rader (eller kolumner) adderas: Determinanten oförändrad.

Dessa egenskaper ger tillsammans en användbar metod som visas i Example 5. Studera detta exempel!

Satser och begrepp: Thm 2.2.1-5, Ex. 5.

Hemuppgifter: 1, 2, 5, 7, 8, 12ac.

2.3 Först formuleras en räkneregel (överst på s. 93) som kan vara värd att lägga märke till:
Om A är en nxn-matris då gäller: det(kA) = kⁿdet(A) Missuppfatta inte Theorem 2.3.1: Relationen det(A+B) = det(A) + det(B) gäller inte.
Thm 2.3.4 uttrycker den viktiga relationen: det(AB) = det(A)det(B).
Ett mycket viktigt resultat bevisas i Thm 2.3.3: A är inverterbar <=> det(A)  0.
Avsnittet avslutas med en del fakta om egenvärden och egenvektorer. Detta kommer vi att studera mer ingående i Kapitel 7 och kan därför tills vidare hoppa över detta stycke.
Thm 2.3.5: det(A^-1) = 1/det(A).
Satser och begrepp: det(kA) = kⁿdet(A) (överst s. 93), Thm 2.3.1, Thm 2.3.3-6.

Hemuppgifter: 1, 2, 3, 4a, 5cd.

3.1
I avsnitt 3.1 introduceras vektorer, en typ av objekt som kan betraktas som riktade sträckor. En vektors komponenter kan ses som de koordinater vektorns ändpunkt har om startpunkten är origo. Observera de två viktiga vektoroperationerna addition och multiplikation med skalär (skalär = tal) samt dessas geometriska tolkning. I tolkningen av vektoraddition framträder vektorernas egenskap att vara flyttbara då man lägger den ena vektorns startpunkt i den andra vektorns ändpunkt.
 

Satser och begrepp: Vektorer och skalärer (s. 117), vektorsumma och skillnad (s. 118-119), produkt med skalär (s. 119), koordinatsystem och komponenter (s. 120), vektoroperationerna på komponentform (s.120-123).

Hemuppgifter: 2a, 3bce, 4b, 6f, 8, 10, 11a.

3.2
Theorem 3.2.1 listar de viktigaste algebraiska reglerna för de operationer som infördes i avsnitt 3.1.

På s. 128 införs begreppet norm för en vektor. Normen för u tolkas geometriskt som längden av u.
 

Satser och begrepp: Thm 3.2.1, norm (s. 128), enhetsvektor (unit vector, s.129).

Hemuppgifter: 1acdf, 2ac, 3abf, 4, 6b.

3.3
Här införs det viktiga begreppet skalärprodukt (dot product). De tre ruturna på s.133 är viktiga. Ur dessa följer en del egenskaper som relaterar skalärproduktens tecken till storleken på vinkeln mellan u och v (Thm 3.3.1). Bl. a: Om skalärprodukten är 0, så är vinkeln rät, (dvs. vektorerna är ortogonala).

Thm 3.3.2 listar några algebraiska regler för skalärprodukten.

Resten av avsnitt 3.3 handlar om projektion. Man definierar vektorn proj_au som projektionen av vektorn u längs vektorn a. Se figurerna på s. 136! Thm 3.3.3 visar hur proj_au kan bestämmas m.hj.a skalärprodukts- och normbegreppet. Lägg både märke till denna formel och till formeln för projektionens längd på s. 137-138.

Satser och begrepp: Definition av skalärprodukt (s.131), skalärprodukt på komponentform (s.133), formeln för 'cosinus för mellanliggande vinkel' (s.133), thm 3.3.1, ortogonala vektorer (s.134), Thm 3.3.2, definition av projektion (s. 136), Thm 3.3.3, projektionsvektorns norm (s. 138), avståndet mellan en punkt och en linje (s.138-139).

Hemuppgifter: 1bd, 2bd, 3bc, 4bd, 5bd, 6ac, 11, 14cd, 15b.

3.4
Definitionen av kryssprodukt ges i boken i tre likvärdiga versioner (två st på s. 141 samt en på s.144). Den på s. 144 är troligen den som är lättast att komma ihåg.

Några algebraiska regler för kryssprodukten finns formulerade iThm 3.4.1 och 3.4.2. Notera särskilt att kryssprodukten uxv är en ny vektor som är vinkelrät mot både u och v.

På s. 145 förekommer en regel som förklarar åt vilket håll uxv pekar i förhållande till u och v. Regeln kallas där 'right-hand rule'. På svenska brukar man tala om 'skruvregeln' som formuleras så här:
uxv pekar åt det håll en (normalgängad) skruv rör sig om den skruvas med den rotationsriktning som svarar mot att u rör sig i riktning mot v. Detta är samma regel som den som anger åt vilket håll z-axeln pekar i ett normalt 3-dimensionellt koordinatsystem. Här definieras skruvriktningen av att positiva x-axeln rör sig i riktning mot positiva y-axeln.

Thm 3.4.3 och fig. 4 på s. 146: längden av vektorn uxv är lika med arean av den parallellogram som spänns upp av u och v.

En viktig geometrisk tolkning tolkning har den s.k. skalära trippelprodukten u^.(vxw), även kallad lådprodukten. Dess belopp, ger nämligen volymen av den parallellepiped som spänns upp av de tre vektorerna i produkten (se figur på s. 149).
Lådprodukten har också den trevliga egenskapen att den kan skrivas som en determinant.
u^.(vxw) är lika med den determinant vars rader består av i tur och ordning u:s, v:s och w:s komponenter. (Se formel (7) på s. 147.)
Ett viktigt specialfall får man då de tre vektorerna ligger i samma plan. I det fallet har ju den uppspända parallellepipeden volymen = 0. Därför får man att determinanten som bildas av de tre vektorerna är = 0 om och endast om de tre vektorerna ligger i samma plan. (Thm 3.4.5).

Satser och begrepp: Kryssprodukten (tre versioner av definitionen. Se särskilt determinantvarianten på s. 144), algebraiska lagar för uxv (Thm 3.4.1 och 3.4.2), skruvregeln som bestämmer uxv:s riktning (right-hand rule, s. 145), ||uxv|| = arean av den av u och v uppspända parallellogrammen (Formel (6), s. 146), skalära trippelprodukten som kan skrivas som en determinant.(s. 147), volymen av den uppspända parallellepipeden (Thm 3.4.4), Thm 3.4.5.

Hemuppgifter: 1abce, 3a, 4b, 7, 8b, 9a, 10b, 11bc, 12.

3.5
Detta avsnitt visar hur ekvationerna för linjer och plan kan skrivas på vektorform.

Ett plan kan med hjälp av sin normalvektor beskrivas av ekvationer som de i formlerna (1) och (2) på s. 155, ekvation (3) i Thm, 3.5.1 , s. 156, och (kanske den mest användbara versionen) (5) på s. 158.

En linje bestäms entydigt av en punkt som ligger på linjen och av linjens riktning. Linjens ekvation på parameterform, (7) på s. 159, och i vektorform, (8) s. 161.

En tillämpning som visas (Thm 3.5.2) är formeln för avståndet mellan en punkt och en linje i 3-dimensionella rummet.

Satser och begrepp: Planets ekvation på komponentform ( (2) s. 155 och (3) s. 156) och vektorform ( (5), s.158 ), linjens ekvation på parameterform ( (7), s.159 ) och vektorform ( (8) s. 160), formeln för avståndet mellan en punkt och en linje i 3 dimensioner.

Hemuppgifter: 1b, 4b, 5b, 6b, 7, 8b, 9b, 11b, 12b, 16a, 39b.

10.1
Komplext tal (def. s. 522), real- och imaginärdel (s.523), addition (s.524) och multiplikation (s. 525).

Satser och begrepp: Komplext tal (def. s. 522), real- och imaginärdel (s.523), addition (s.524) och multiplikation (s. 525).

Hemuppgifter: 3a, 4, 6b, 8b, 9b, 10c, 14, 17.

10.2
Satser och begrepp: z-konjugat (s.528), beloppet av z (Modulus, s. 529), Thm 10.2.1-3 , ex.3 s.531.

Hemuppgifter: 1bde, 2bde, 3b, 4bd, 5b, 6c, 11, 12.

10.3
Här införs den viktiga polära formen för komplexa tal (2) s. 536. Studera Ex. 2 på s. 538 där multiplikation och division utförs m.hj.a. övergång till polär form.

DeMoivre's formel, (6) s. 539, visar hur potensuttryck som zⁿ lätt kan återföras på normalform.

Avslutningsvis visas hur man löser s.k. binomiska ekvationer zⁿ = w, Ex 3 s. 541. Det visar sig att rötterna till sådana ekvationer alltid bildar regelbundna n-hörningar i det komplexa planet, Fig. 5 s. 541.

Satser och begrepp: Polär form (s. 536), DeMoivre's formel (s. 539), binomiska ekvationer och deras lösning (s. 540+Ex.3,4 s. 541).

Hemuppgifter: 1, 3df, 4cd, 6b, 7bd.

Kompletteringskompendiet avsnitt 2.
Avsnittet börjar med att definiera begrepp som polynom, polynomfunktion och polynomekvation, ett polynoms nollställen eller rötter.

En metod att lösa andragradsekvationer med komplexa koefficienter ges i Exempel 2.1. Studera särskilt hur kvadratkomplettering används innan den nya variabeln w införs.

Exempel 2.2 presenterar en algoritm för polynomdivision. Har du lärt dig en annan metod gör inte det något.

Satserna 2.3 och 2.4 sammanfattar fakta om polynomdivision (2.3) och sambandet mellan ett polynoms nollställen och dess faktorer (2.4).

Sats 2.5 är den klassiska Algebrans fundamentalsats som hävdar att varje ickekonstant polynom har minst ett komplext nollställe.

Detta medför att varje polynom av grad n har exakt n st. komplexa nollställen (med multipliciteterna inräknade), Sats 2.6.

I tillämpningar dyker oftast upp polynomekvationer med reella koefficienter. För sådana gäller den viktiga regeln att de ickereella nollställena alltid förekommer i konjugerade par (Sats 2.8).

Detta leder till slutsatsen att ett reellt polynom kan skrivas som produkten av rella faktorer av högst andra graden (Sats 2.10).

Satser och begrepp: Polynom, polynomekvation och nollställe, metoden att lösa andragradsekvationer med komplexa koefficienter, polynomdivisionsalgoritmen (Sats 2.3), faktorsatsen (Sats 2.4), multipliciteten hos ett nollställe, algebrans fundamentalsats (Sats 2.5), n:egradspolynom som produkt av n st. faktorer (Sats 2.6), för reella polynom bildar de ickereella nollställena konjugerade par (Sats 2.8), ett reellt ickekonstant polynom kan skrivas som produkten av reella faktorer av grad 1 eller 2. (Sats 2.10).

Hemuppgifter: 2.1e, 2.2cef, 2.3bc, 2.4a, 2.7, 2.12, 2.11, 2.13, 2.16, 2.19cd.

4.1 I kapitel 4 förekommer en hel del stoff som tidigare behandlats i 2 eller 3 dimensioner. Avsnittet ger i stort sett en repetition av Kap. 3.1 - 3.3 men i n dimensioner. Notera att kryssprodukten inte låter sig generaliseras, den är bunden till 3 dimensioner. Notera också de båda olikheterna Cauchy-Schwarz' olikhet (Thm 4.1.3) och triangelolikheten (Thm 4.1.5d), som båda kan formuleras i n dimensioner.

I slutet av kapitlet förekommer några diskussioner som relaterar inre produkten till matrismultiplikation. Studera dels användningen av transponerade vektorer i uttrycken för inre produkter på s. 176 och dels matrisprodukten nederst på s. 177 där varje element i produkten är skriven som en inre produkt.

Satser och begrepp: n-dimensionell vektor, Euklidisk inre produkt (skalärprodukt), norm i n dimensioner, Euklidisk distans, Cauchy-Schwarz' olikhet (Thm 4.1.3), triangelolikheten (Thm 4.1.5d), inre produkt och matrismultiplikation (s. 176-178).

Hemuppgifter: 1cf, 2, 6ab, 8, 9ab, 11abd, 14abd.

4.2
Detta ganska långa avsnitt innehåller dels en diskussion om linjära transformationer i allmänhet och dels en ingående genomgång av olika typer av enkla geometriska transformationer (spegling, projektion, rotation m.m.)

Till att börja med införs distinktionen mellan en mxn-matris A och den linjära transformation T_A som A definierar. Om istället namnet T på transformationen är givet, kan man kalla motsvarande matris [T] (s. 183).

På sidorna 185 - 192 följer sedan genomgången av de enkla transformationerna och deras matriser. Detta beskrivs både i fallen T: R² -> R² och T: R³ -> R³.

Slutligen införs på s. 192 - 195 begreppet komposition av transformationer.

Den linjära transformationen T_A definierad av mxn-matrisen A, T_A : R^m -> Rⁿ, matrisen [T] som definierar transformationen T, reflektion omkring koordinataxlar (R²->R² ), reflektion omkring koordinatplan (R³->R³ ), ortogonal projektion på koordinataxlar (R²->R² ), ortogonal projektion på koordinatplan (R³->R³ ), rotation i planet (R²->R² ), rotation omkring en koordinataxel (R³->R³ ), förminskning/förstoring med given faktor (R²->R² och R³->R³ ), begreppet komposition T_{B °}T_A.

Satser och begrepp: Den linjära transformationen T_A definierad av mxn-matrisen A, T_A : R^m -> Rⁿ, matrisen [T] som definierar transformationen T, reflektion omkring koordinataxlar (R²->R²), reflektion omkring koordinatplan (R³->R³), ortogonal projektion på koordinataxlar (R²->R²), ortogonal projektion på koordinatplan (R³->R³), rotation i planet (R²->R²), rotation omkring en koordinataxel (R³->R³), förminskning/förstoring med given faktor (R²->R² och R³->R³), komposition T_{B °}T_A.

Hemuppgifter: 1ab, 2cd, 4bd, 5a, 6bc, 7a, 8b, 9b, 10, 12b, 13a, 17b.

9.2
Detta avsnitt är avsett att komplettera genomgången i kapitel 4 av de geometriska matristransformationer. Avsnittet berör uteslutande transformationer från R² till R².

Man studerar effekterna av de tre typerna av elementära matriser och finner att i fallet R² -> R² svarar de mot antingen reflektion eller förstoring/förminskning eller skjuvning (shear). På s. 451 finns klargörande figurer som beskriver detta.

Man vet sedan tidigare (Kap. 1.5, Thm 1.5.3) att inverterbara matriser A alltid kan skrivas som en produkt av elementära matriser. Därför blir den geometriska effekten av en transformation T_A densamma som en följd av elementära transformationer av dessa tre typer. Detta formuleras i Theorem 9.2.1.

I Theorem 9.2.2 formuleras hur multiplikation med inverterbara matriser påverkar linjer, parallella linjer och linjesegment. Sammanfattningsvis gäller att punkter som före transformationen ligger på samma linje gör så även efter.

Satser och begrepp: Skjuvning som effekt av en elementär matris, Thm 9.2.1 (effekt av inverterbara matriser), Thm 9.2.2 (effekt av inverterbara matriser på linjer).

Hemuppgifter: 1, 4, 6e, 8ab, 9, 10, 11b, 12bd, 13b, 14, 17e.

4.3
I detta avsnitt genomgås några viktiga egenskaper hos linjära transformationer. Bl.a. karakteriseras de linjära transformationerna på ett sätt som egentligen utgör den vanligaste definitionen av sådana transformationer (Theorem 4.3.2, s.203).

Thm 4.3.3 beskriver ett sätt att finna standardmatrisen [T] för T : Rⁿ -> R^m.

Avsnittet slutar med ett omnämnande av egenvärden och egenvektorer, vilket vi dock kan hoppa över eftersom dessa begrepp behandlas mer ingående i kapitel 7.

Satser och begrepp: 'T is one-to-one' (T är injektiv), ' the range of T is Rⁿ' (T är surjektiv),invers av T, Thm 4.3.1-4.

Hemuppgifter: 1cdefg, 2bc, 4, 5b, 6ac, 10, 13b.

Kompletteringskompendiet avsnitt 3.
Hela avsnittet bör läsas mycket noga.

Hemuppgifter i läroboken: 5.2  7ad, 8ad, 11bd, 14ac;  5.3  2ac, 3bcd, 8;  5.4  2bc, 3bcd, 20ab;

7.1
I detta avsnitt inför man de viktiga begreppen egenvärde och egenvektor. (Läs gärna den kursiva texten alldeles under rubriken på s. 355. Där finns en imponerande lista på tillämpningsområden för dessa begrepp.)

Egenvärden kan vara reella eller komplexa, ickereella tal. I denna kurs behandlas endast det reella fallet. I tre dimensioner finns alltid minst ett reellt egenvärde. I Ex. 2 s.357 visas hur tre, i detta fall reella, egenvärden räknas fram. Här finns det också en diskussion om hur man kan gissa heltalslösningar till en polynomekvation.
Ex. 5 visar hur matrisens egenvektorer bestäms då egenvärdena är kända. Tekniken att räkna fram egenvektorer är naturligtvis viktig. Man noterar att det gäller att lösa ekvationssystem med oändligt många lösningar. Observera också att om x är en egenvektor så är alltid också kx (k skalär) en egenvektor. Det finns alltså alltid oändligt många egenvektorer.

 Man skall vara särskilt uppmärksam vid bestämning av egenvektorer som svarar mot multipla egenvärden (egenvärden som är multipla nollställen till den karakteristiska ekvationen).

I Thm 7.1.3 formuleras observationen att om  är ett egenvärde till A och om x är en motsvarande egenvektor, så är ^k ett egenvärde till matrisen A^k, medan x fortfarande är en motsvarande egenvektor.

Avsnittet slutar med en diskussion av de fall då egenvärdet  = 0. I Thm. 7.1.4 visar man att A är inverterbar om och endast om inget egenvärde är lika med 0.

I Thm 7.1.5 adderas resultatet i Thm. 7.1.4 till den numera mycket långa listan på ekvivalenta egenskaper hos kvadratiska matriser.

 Satser och begrepp: Egenvärde s. 355, egenvektor s.355, egenvärdena är lösningar till karakteristiska ekvationen det(I - A) = 0, att bestämma egenvärdena till A (Ex.2 s. 357), egenvärdena till triangulära matriser finns i diagonalen (Thm. 7.1.1), att bestämma egenvektorerna till A svarande mot egenvärdet  (Ex. 5 s.359), A^k har egenvärdet ^k (Thm. 7.1.3), A är inverterbar om och endast om inget egenvärde är 0 (Thm. 7.1.4), listan på ekvivalenta villkor (Thm 7.1.5).

Satser och begrepp: Egenvärde (s. 355), egenvektor (s.355), karakteristisk ekvation, att bestämma egenvärdena till A (Ex.2 s. 357), egenvärdena till triangulära matriser (Thm. 7.1.1), att bestämma egenvektorerna till A svarande mot egenvärdet (Ex. 5 s.359), A^k har egenvärdet ^k (Thm. 7.1.3), A är inverterbar om och endast om inget egenvärde är 0 (Thm. 7.1.4), listan på ekvivalenta villkor (Thm 7.1.5).

Hemuppgifter: 1a, 3cde, 4a, 5a, 6c, 18.

7.2
I föregående avsnitt visades exempel på att en nxn-matris A hade n st. linjärt oberoende vektorer, men det fanns också exempel på att detta antal var mindre. I avsnitt 7.2 formuleras detta som egenvektorproblemet:
Existerar det n st. linjärt oberoende egenvektorer till nxn-matrisen A?

Detta problem visar sig vara relaterat till diagonaliseringsproblemet:
Finns det en inverterbar matris P som diagonaliserar nxn-matrisen A, så att P^-1AP blir en diagonalmatris ?

Om A är diagonaliserbar existerar alltsåt diagonalmatrisen D = P^-1AP som har en del liknande egenskaper som A, bl.a. har A och D samma egenvärden.

Thm 7.2.1. utsäger att egenvektorproblemet och diagonaliseringsproblemet är ekvivalenta: A har n st. linjärt oberoende egenvektorer <=> A är diagonaliserbar.

På s. 367 beskrivs metoden att diagonalisera en matris A.

Ex. 1, 2, s.367-368, är exempel på diagonaliseringar av 3x3-matriser där matrisen i båda fallen har ett enkelt och ett dubbelt egenvärde.

För diagonaliseringsproblemet är det alltså väsentligt att veta om det går att hitta maximalt antal linjärt oberoende egenvektorer. Thm 7.2.2 och Thm 7.2.3 ger ett viktigt tillräckligt villkor för detta.

Avsnittet slutar med en tillämpning av diagonalisering: Beräkning av matrispotenser A^k för diagonaliserbara matriser A.

Satser och begrepp: Egenvektorproblemet, diagonaliseringsproblemet, Thm 7.2.1, att diagonalisera en matris, Thm 7.2.2-3, formeln A^k = PD^kP^-1.

Hemuppgifter: 2, 3, 5, 9, 10, 14, 20b.

9.6
Detta avsnitt utgör en tillämpning av diagonaliseringsmetoden som behandlades i 7.2. Dock bygger det något på stoff som formellt inte tillhör kursen. Detta bör man känna till:

En kvadratisk form är ett variabeluttryck av enbart andragradstermer som alltså kan definieras av ett uttryck av typen x^TAx där variablerna är komponenterna i vektorn x^T = [x₁ x₂ ... x_n] och A en symmetrisk nxn-matris.

I en mängd ortonormerade vektorer är alla inbördes ortogonala och har längden = 1.

'Ortogonalt diagonaliserbar' innebär att A är diagonaliserbar av en ortogonal matris, dvs av en matris vars kolumner (och därmed även rader) är ortonormerade.

För en ortogonal matris P gäller P^T = P^-1, vilket innebär att P^TP = I som i sin tur leder till att det(P) = +1 eller -1.

Geometriskt sett definierar ortogonala matriser transformationer som kan beskrivas som stela vridningar (+ev speglingar) och som lämnar de transformerade vektorernas längder oförändrade.

Om A är en symmetrisk nxn-matris så har A n st. ortonormerade egenvektorer och är därmed ortogonalt diagonaliserbar.

Thm 9.6.1 beskriver hur diagonaliseringstekniken från kapitel 7 kan användas till att avlägsna blandade termer från kvadratiska former.

Därefter behandlas i 9.6, med viss utförlighet, de s.k koniska sektionerna, dvs de plana kurvor som uppstår då en kon (egentligen en dubbelkon dvs. två koner med samma centralaxel och med motriktade spetsar) snittas av ett plan.
Ekvationerna för dessa kurvor är alltid polynomekvationer av andra graden. Om kurvornas symmetriaxlar lutar i förhålande till x- och/eller y-axeln förekommer den blandade termen 'xy' i ekvationen.
Det blir alltså ett diagonaliseringsproblem att finna en substitution som får denna xy-term att försvinna. Geometriskt innebär detta att man vrider koordinatsystemet så att någon av kurvans symmetriaxlar blir parallell med x- eller y-axeln.

På s. 489-490 redogörs för en diagonaliseringsmetod som i stort sett är analog med den som behandlades i 7.2.

Satser och begrepp: Thm 9.6.1, konisk sektion, ekvationens associerade kvadratiska form, diagonaliseringsmetoden (s. 489 - 490. Obs det(P) = +1), Thm 9.6.2 (Principalaxelsatsen).

Hemuppgifter: 1ac, 6bcfg, 7bd, 8a, 10, 11.

9.7
Detta avsnitt behandlar andragradsytor i R³ på samma sätt som avsnitt 9.6 behandlar andragradskurvor i R². Fig. 1 på s. 496 ger en översikt över de sex viktigaste typerna av andragradsytor.

I övrigt presenteras samma teori som i 9.6 om diagonalisering av ytornas associerade kvadratiska former.

Metoden anges på s. 497 inklusive föreskriften att den diagonaliserande ortogonala matrisen ska ha determinanten = 1.

Thm. 9.7.1 formulerar motsvarande principalaxelteorem som anger att diagonaliseringen kan åstadkommas av en ortogonal matris med determinanten = 1.

Satser och begrepp: De olika typerna av andragradsytor (Fig.1, s. 496), diagonaliseringsmetoden (s. 497), Thm. 9.7.1 (Principalaxelteoremet för andragradsytor).

Hemuppgifter: 6ad, 8, 9, 10.