Vädret...
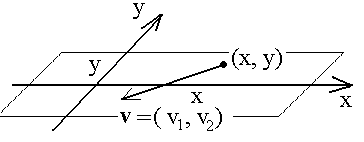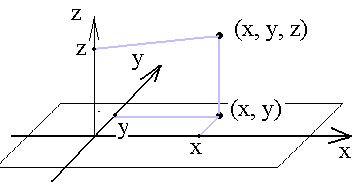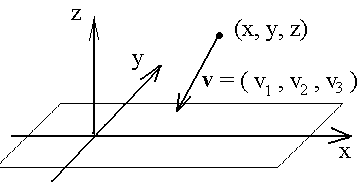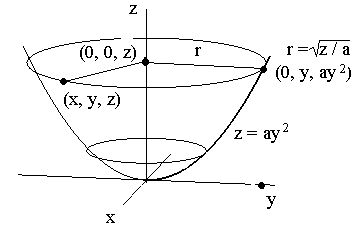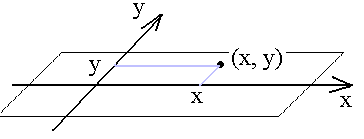
	Vi vill beskriva vädret över ett litet område av jordklotet och föreståller oss detta som plant. När vi lagt in ett koordinatsystem som i figurer kan vi tala om punkters (orters) koordinater
Vi låter T ( x, y ) vara temperaturen i pukten med koordinater ( x, y ) . Detta är en funktion som till punkter i planet ordnar ett reellt tal. En funktion av flera (två) variabler.

Men... Tiden spelar roll.
Men temperaturen beror ju inte bara på var man befinner sig utan också på när man är på platsen. Det är mer realistiskt att se temperaturen som en funktion av tre variabler ( x, y, t ) där t anger tiden	Funktionen T är en reellvärd funktion av tre rella variabler.

Men... Vädret är mer än temperatur.
Luftfuktigheten och lufttrycket är väsentlig. Så ... Vi låter f ( x, y, t ) och p ( x, y, t ) beteckna luftfuktigheten i punkten ( x, y ) vid tiden t .	Funktionerna f och p är också reellvärda funktion av tre reella variabler.

Men.. Vinden då?

I varje punkt finns en vindriktning och en vindstyrka. Vinden i punkten ( x, y ) vid tiden t av en vektor v med två koordinater v₁ och v₂ .

Var och en av dessa är reellvärda funktioner av tre reella variabler

v₁( x, y, t) och v₂( x, y, t)

Vinden v är en vektorvärdfunktion av tre reella variabler.

v ( x, y, t ) = (v₁ ( x, y, t ), v₂ ( x, y, t ))

Men... De högre luftlagren då ?
Vinden blåser ju i olika riktningar på olika höjd över jordytan och temperatur och tryck varierar också med höjden.
	Vi behöver en z -koordinat för att mäta detta.
	Viden anges nu med en vektor med tre koordinater v = ( v₁, v₂, v₃ )
Funktionerna T , f , p, v₁ , v₂ och v₃ är nu reellvärda funktioner av fyra reella variabler ( x, y, z, t ).

	Kurvan z = ay² roterar kring z-axeln.
	Kurvan z = ay² roterar kring y-axeln.

Grafen till en reellvärd funktion av två reella variabler

	Ovan för punkten ( x, y, 0 ) i x, y -planet markeras punkten ( x, y, f ( x, y )) .
	Definitionsmängden till funktionen lever i x, y -planet.