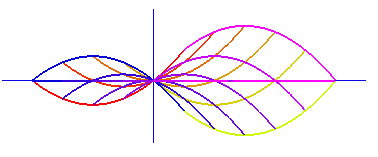
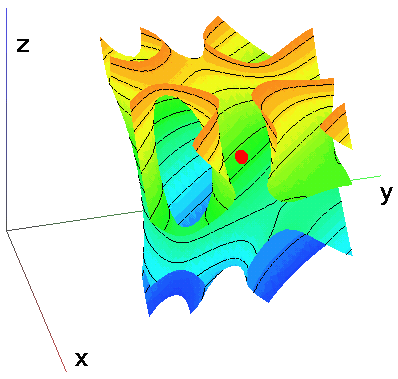
Figuren visar nivåytan
F( x, y, z) = 3 sin(25/4)
där
F( x, y, z) = sin(xy) + sin(yz) + sin(xz) .
På ytan har punkten a = ( 5/2, 5/2, 5/2)
markerats.
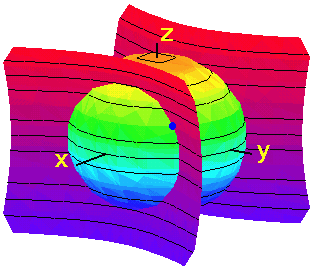
Eftersom Fz'( a)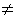 0 kan man i en
omgivning till
( x, y) = ( 5/2, 5/2)
finna en (C1-)funktion
f( x, y) med 0 kan man i en
omgivning till
( x, y) = ( 5/2, 5/2)
finna en (C1-)funktion
f( x, y) med
- f( 5/2, 5/2) = 5/2
- F( x, y, f( x, y)) = 3 sin(25/4)) .
Variabeln z är
alltså i sambandet som ger nivåytan
lokalt kring a en funktion av de övriga
variablerna.
Derivering av 2) ger enligt kedjeregeln
- Fx'+Fz'fx' = 0
- Fy'+Fz'fy' = 0
som leder till
fx'( 5/2, 5/2) = fy'( 5/2, 5/2) = -1.
Detta ger Taylorutvecklingen
f( x, y) = 5/2 - (x - 5/2) - (y - 5/2) + |(x,y)-(5/2, 5/2)|2B( x, y) ,
där B är begränsad nära
( 5/2, 5/2) .
|
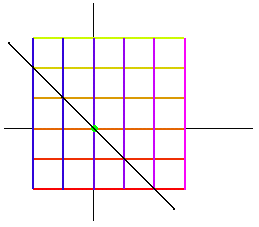
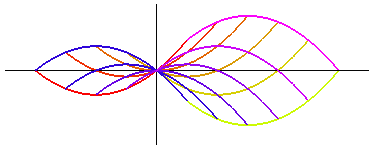
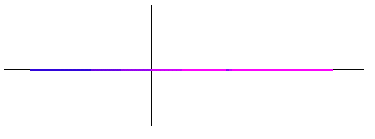
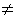 0 kan man i en
omgivning till
( x, y) = ( 5/2, 5/2)
finna en (C1-)funktion
f( x, y) med
0 kan man i en
omgivning till
( x, y) = ( 5/2, 5/2)
finna en (C1-)funktion
f( x, y) med
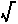 ((28-z2)/3)
((28-z2)/3)