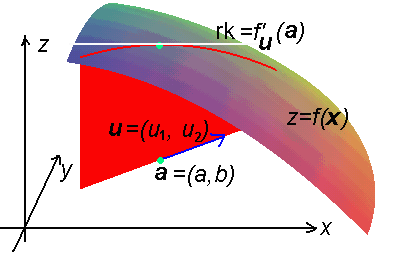
Riktningsderivata

Funktionen  f(x)  har riktningsderivata i  a  i riktningen  u  om gränsvärdet av f(a+tu) - f(a) t när  t  går mot  0  existerar.   Gränsvärdet betecknas då fu'(a) och kallas riktningsderivatan av  f(x)  i  a  i riktingen  u .   När  f(x)  är differentierbar i  a  kan riktningsderivatan beräknas som fu'(a) = gradf(x)·u .

---

 

Alla riktnigsderivator men ej differentierbar

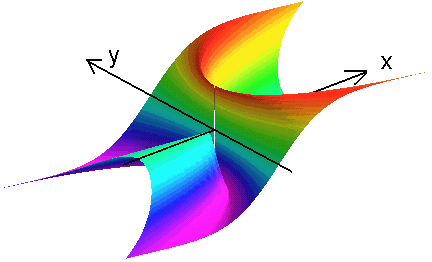
Figuren illustrerar grafen till  f(x, y) = xy2/ (x2 + y4)  där man satt  f(0, 0) = 0 . En kalkyl, enligt gränsvärdesdefinitionen av riktningsderivata, visar att funktionen har riktningsderivata i varje riktning  u = (u1, u2)  i origo och   fu'(0, 0) =  u22/ u1  när  u1  0 0  när  u1 = 0 Funktionen är inte kontinuerlig i origo och kan därför inte vara differentierbar där.

---

Gradienten (två variabler)

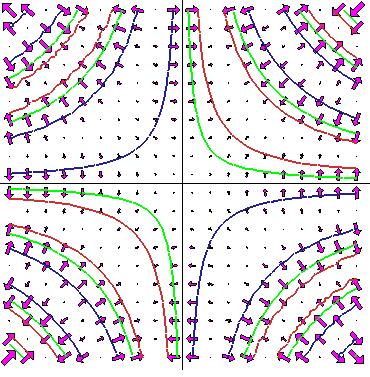Figuren illustrerar gradienten till  f(x, y) = sin(xy) . I punkten  (x, y)  har vektorn  grad f(x, y)  avsats. Nivåkurvor har till funktionen har också markerats i olika färger. Gradienterna är vikelrät mot nivåkurovorna. Grafen till samma funktion se ut så här

---

 

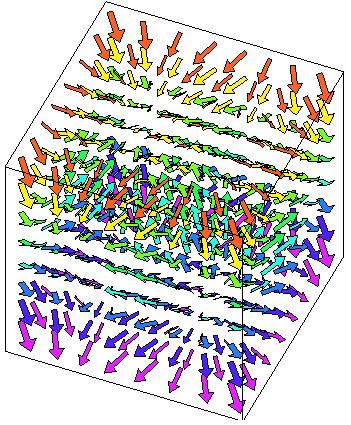
Gradienten (tre variabler)

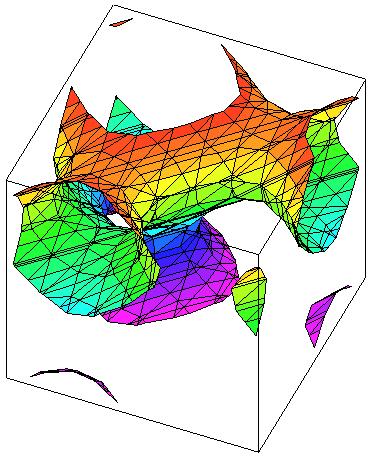Figuren illustrerar gradienten till  f(x, y, z) = sin(x) + sin(y) + sin(z) . I punkten  (x, y, z)  har vektorn  grad f(x, y, z)  avsats. Gradienterna är vikelrät mot nivåytor. Nivåytan  f(x, y, z) = 0.4  till samma funktion ses till höger.

---

 

Varning om andraderivator

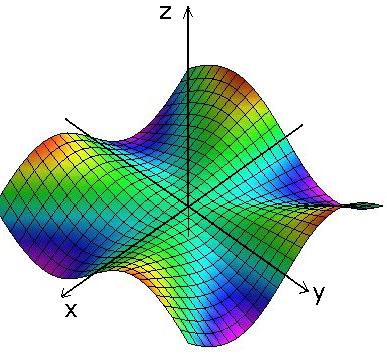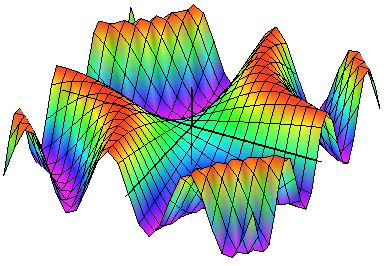
Figuren illustrerar grafen till  f(x, y) = xy(x2 - y2) /(x2 + y2) .   En kalkyl visar att  fx'(0,0) = 0 = fy'(0,0)  och att  fxy''(0,0) = 1 , men att  fyx''(0,0) = -1 .   När andraderivatorna  fxy''  och  fyx''  är kontinuerliga i en omgivning till en punkt är de också lika där

---